ЬтФПФкШн
ЁОЬтФПЁПФГЫЎЕчеОаЫНЈСЫвЛИізюДѓаюЫЎШнСПЮЊ12ЭђУз3ЕФаюЫЎГиЃЌВЂХфга2ИіСїСПЯрЭЌЕФНјЫЎПкКЭ1ИіГіЫЎПкЃЎФГЬьДг0ЪБжС12ЪБЃЌНјааЛњзщЪддЫаа.ЦфжаЃЌ0ЪБжС2ЪБДђПЊ2ИіНјЫЎПкНјЫЎЃЛ2ЪБЃЌЙиБе1ИіНјЫЎПкМѕЛКНјЫЎЫйЖШЃЌжСаюЫЎГижаЫЎСПДяЕНзюДѓаюЫЎШнСПКѓЃЌЫцМДЙиБеСэвЛИіНјЫЎПкЃЌВЂДђПЊГіЫЎПкЃЌжБжС12ЪБаюЫЎГижаЕФЫЎЗХЭъЮЊжЙ.
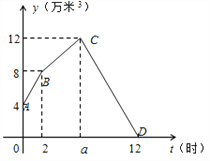
Шєет3ИіЫЎПкЕФЫЎСїЖМЪЧдШЫйЕФЃЌЧв2ИіНјЫЎПкЕФЫЎСїЫйЖШвЛбљЃЌЫЎГижаЕФаюЫЎСП yЃЈЭђУз3ЃЉгыЪБМфtЃЈЪБЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌЧыИљОнЭМЯѓНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉаюЫЎГижадгааюЫЎ ЭђУз3ЃЌаюЫЎГиДязюДѓаюЫЎСП12ЭђУз3ЕФЪБМфaЕФжЕЮЊ ЃЛ
ЃЈ2ЃЉЧѓЯпЖЮBCЁЂCDЫљБэЪОЕФyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉаюЫЎГижааюЫЎСПЮЌГждкmЭђУз3вдЩЯЃЈКЌmЭђУз3ЃЉЕФЪБМфга3аЁЪБЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЌ6ЃЛЃЈ2ЃЉyBC=x+6ЃЌЃЈ2ЁмxЁм6ЃЉЃЛ![]() .ЃЈ6ЁмxЁм12ЃЉ;(3)10
.ЃЈ6ЁмxЁм12ЃЉ;(3)10
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнКЏЪ§ЭМЯѓПЩвдЕУЕНаюЫЎГижадгааюЫЎЕФЬхЛ§ЃЌгЩ2ИіСїСПЯрЭЌЕФНјЫЎПкКЭЭМЯѓПЩвдЧѓЕУaЕФжЕЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓПЩвдЗжБ№ЧѓЕУЯпЖЮBCЁЂCDЫљБэЪОЕФyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃЌBCЩЯЕФКЏЪ§жЕКЭCDЩЯЕФКЏЪ§жЕЯрЕШЃЌЧвЗжБ№ЖдгІЕФЪБМфВюжЕЮЊ3ЃЌДгЖјПЩвдЧѓЕУmЕФжЕЃЎ
НтЃК(1)гЩЭМЯѓПЩжЊ,аюЫЎГижадгааюЫЎ4ЭђУз3,
аюЫЎГиДязюДѓаюЫЎСП12ЭђУз3ЕФЪБМфaЕФжЕЮЊЃК2+(128)ЁТ(842ЁС12)=6ЃЌ
ЙЪД№АИЮЊЃК4ЃЌ6ЃЛ
(2)ЁпB(2,8),C(6,12),ЩшжБЯпBCЕФКЏЪ§ЙиЯЕЪНЮЊy=k1x+b1ЃЌ
гЩЬтвт,ЕУ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() .
.
МДжБЯпBCЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊy=x+6(2x6)ЃЌ
ЁпC(6,12),D(12,0),ЩшжБЯпCDЕФКЏЪ§ЙиЯЕЪНЮЊy=k2x+b2ЃЌ
гЩЬтвт,ЕУ![]() ЃЌ
ЃЌ
НтЕУЃК ![]() .
.
МДжБЯпCDЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊy=2x+24(6x12)ЃЛ
(3)ЩшдкBCЩЯаюЫЎСПДяЕНmЭђУз3ЕФЪБМфЮЊt,дђдкCDЩЯаюЫЎСПДяЕНmЭђУз3ЕФЪБМфЮЊ(t+3)hЃЌ
гЩЬтвт,ЕУt+6=2(t+3)+24ЃЌ
НтЕУЃКt=4ЃЌ
ЁрЕБ t=4ЪБЃЌy=4+6=10
МДmЕФжЕЪЧ10.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ