Question

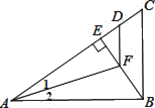
【题目】如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.

(1)如果△ABC的周长为14cm,AC=6cm,那么△ABE的周长=____;

(2)你发现线段AB与BD的和等于图中哪条线段的长?请证明你的结论.

Answer 1

【答案】8cm

【解析】

（1）通过线段的等量代换即可求解；
（2）由AD⊥BC，BD=DE，点E在AC的垂直平分线上，根据线段垂直平分线的性质，可得AE=EC，AB=AE，继而证得AB+BD=AE+DE=DC．

(1) ∵点E在AC的垂直平分线上，

∴AE＝CE，

∵AD⊥BC

∴∠ADB＝∠ADE

在△ABD和△ADE中

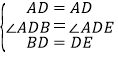
∴△ABD≌△ADE（SAS）

∴AB＝AE，

又∵△ABE的周长是：AB+BE+AE,

∴△ABE的周长=AB+BE+CE=AB+BC,

∵△ABC的周长为14cm，AC=6cm，
∴AB+BC=14-6=8，
∴△ABE的周长=AB+BC=8cm．
故答案为：8；

(2) AB+BD=DC.证明如下:

∵AD⊥BC,BD=DE,AD=AD,

∴△ABD≌△AED(SAS)，

∴,AB=AE.

又∵点E在AC的垂直平分线上,

∴AE=EC,

∴AB=EC.

∴AB+BD=EC+DE=DC.