题目内容
【题目】综合题。
(1)计算题:|﹣3|+ ![]() tan30°﹣
tan30°﹣ ![]() ﹣(2017﹣π)0+(
﹣(2017﹣π)0+( ![]() )﹣1
)﹣1
(2)计算题:(x﹣2﹣ ![]() )÷
)÷ ![]()
(3)解不等式组:  .
.
【答案】
(1)解:|﹣3|+ ![]() tan30°﹣
tan30°﹣ ![]() ﹣(2017﹣π)0+(
﹣(2017﹣π)0+( ![]() )﹣1
)﹣1
=3+ ![]() ﹣2﹣1+3
﹣2﹣1+3
=3+1﹣2﹣1+3
=4
(2)解:x﹣2﹣ ![]() )÷
)÷ ![]()
= ![]()
= ![]()
=﹣(x+4)
=﹣x﹣4
(3)解: 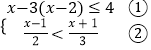
解不等式①,得
x≥1,
解不等式②,得
x<5,
∴原不等式组的解集是1≤x<5
【解析】(1)根据绝对值、特殊角的三角函数值、零指数幂、负整数指数幂可以解答本题;(2)根据分式的减法和除法可以解答本题;(3)根据解一元一次不等式组的方法可以解答本题.
【考点精析】根据题目的已知条件,利用分式的混合运算和零指数幂法则的相关知识可以得到问题的答案,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数).

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖 | 二等奖 | 三等奖 |
1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
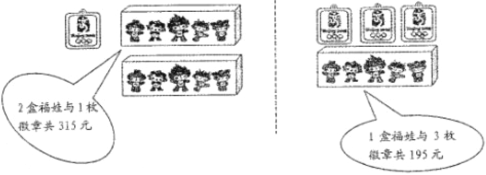
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?







