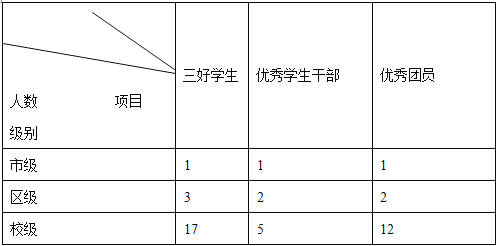
题目内容
【题目】如图，已知抛物线经过A（﹣2，0）B（﹣3，3）及原点O，顶点为C．
（1）求抛物线的解析式；
（2）若点E在抛物线的对称轴上，且A、O、D、E为顶点是四边形是平行四边形，求点D的坐标．
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？
【答案】
（1）
解：设抛物线的解析式为y=ax2+bx+c（a≠0），
将点A（﹣2，0），B（﹣3，3），O（0，0），代入可得：
，
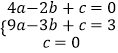解得： 
，
所以函数解析式为：y=x2+2x
（2）
解：①以AE为边时，∵A，O，D，E为顶点的四边形是平行四边形，
∴DE=AO=2，D在x轴向方不可能，
∴D在x轴上方，且DE=2，当D点在对称轴直线x=﹣1的右侧时，D的坐标为（1，3）；
当D点在对称轴直线x=﹣1的左侧时，根据二次函数图象的对称性可知点D的坐标为（﹣3，3），
②以AO为对角线时，则DE与AO互相平分，
∵点E在对称轴上，且线段AO的中点横坐标为﹣1，
由对称性可知，符合条件的点D只有一个，与点C重合，即C（﹣1，﹣1），
综上点D的坐标为（1，3）或（﹣3，3）（﹣1，﹣1）
（3）
解：假设存在点P，使以P，M，A为顶点的三角形与△BOC相似，如图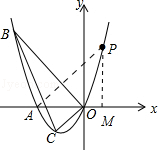 
，
设P（x，y），由题意知x＞0，y＞0，且y=x2+2x，
由题意，△BOC为直角三角形，∠COB=90°，且OC：OB=1：3，
①若△PMA∽△COB，则 
= 
，
即x+2=3（x2+2x），得
x1= 
，x2=﹣2（舍去），当x= 时，y= 
，即P（ ， ）；
②若△PMA∽△BOC， 
= 
，
即：x2+2x=3（x+2），
得：x1=3，x2=﹣2（舍去）当x=3时，y=15，即P（3，15）
故符合条件的点P有两个，分别（ ， ）或（3，15）
【解析】（1）设抛物线的解析式为y=ax2+bx+c（a≠0），把点A（﹣2，0），B（﹣3，3），O（0，0），代入求出a，b，c的值即可；（2）首先由A的坐标可求出OA的长，再根据四边形AODE是平行四边形，D在对称轴直线x=﹣1右侧，进而可求出D横坐标为：﹣1+2=1，代入抛物线解析式即可求出其横坐标；根据平行四边形的对角线互相平分，可得答案；（3）分△PMA∽△COB和△PMA∽△BOC表示出PM和AM，从而表示出点P的坐标，代入求得的抛物线的解析式即可求得t的值，从而确定点P的坐标．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
