题目内容
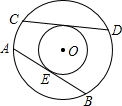
已知：如图，同心圆O，大圆的弦AB=CD，且AB是小圆的切线，切点为E．求证：CD是小圆的切线．
证明：如右图所示，连接OE，过O作OF⊥CD于F．
∵AB与小⊙O切于点E，
∴OE⊥AB，
∵AB=CD，
∴OE=OF（同圆等弦的弦心距相等），
∴CD与小⊙O相切．
分析：要证CD是小圆的切线，过O作OF⊥CD于F，AB与小⊙O切于点E，根据同圆等弦的弦心距相等可知OE=OF．
点评：题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线；解决问题的关键是同圆等弦的弦心距相等．
∵AB与小⊙O切于点E，
∴OE⊥AB，
∵AB=CD，
∴OE=OF（同圆等弦的弦心距相等），
∴CD与小⊙O相切．
分析：要证CD是小圆的切线，过O作OF⊥CD于F，AB与小⊙O切于点E，根据同圆等弦的弦心距相等可知OE=OF．
点评：题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线；解决问题的关键是同圆等弦的弦心距相等．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
已知：如图，两个以O为圆心的同心圆，AB是大圆的直径，弦BC切小圆于点D，CE⊥AB，垂足为E，大圆的直径为25，小圆的直径为15米．求AE的长．
已知：如图，同心圆O，大圆的弦AB=CD，且AB是小圆的切线，切点为E．求证：CD是小圆的切线．
5、已知：如图是两个同心圆被两条半径截得的一个扇形图．请你画出一个以O为对称中心的扇形的对称图形（保留画图痕迹，写出画法）