题目内容
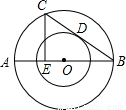
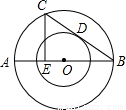
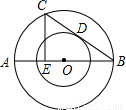
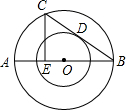 已知:如图,两个以O为圆心的同心圆,AB是大圆的直径,弦BC切小圆于点D,CE⊥AB,垂足为E,大圆的直径为25,小圆的直径为15米.求AE的长.
已知:如图,两个以O为圆心的同心圆,AB是大圆的直径,弦BC切小圆于点D,CE⊥AB,垂足为E,大圆的直径为25,小圆的直径为15米.求AE的长.
分析:要求AE的长,需作辅助线,连接OD和AC,根据题意利用勾股定理,在三角形ODB中,可求出BD,进而得到BC,同理在三角形ACB中,可求出AC,然后利用△ACE∽△ABC,通过比例线段,求出AE的长.
解答: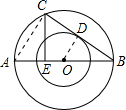 解:连接OD、AC,
解:连接OD、AC,
∵BC切小圆于点D
∴OD⊥BC
又∵OB=12.5,OD=7.5
∴BD=
=10
因此根据垂径定理知BC=20
在RT△ABC中,AC=
=
=15
又∵AB为圆的直径,且CE⊥AB,
∴∠ACB=∠CEB=90°,又∠ABC=∠CBE,
∴△ACE∽△ABC
∴
=
即
=
∴AE=9.
 解:连接OD、AC,
解:连接OD、AC,∵BC切小圆于点D
∴OD⊥BC
又∵OB=12.5,OD=7.5
∴BD=
| 12.52-7.52 |
因此根据垂径定理知BC=20
在RT△ABC中,AC=
| AB2-BC2 |
| 252-202 |
又∵AB为圆的直径,且CE⊥AB,
∴∠ACB=∠CEB=90°,又∠ABC=∠CBE,
∴△ACE∽△ABC
∴
| AC |
| AB |
| AE |
| AC |
即
| 15 |
| 25 |
| AE |
| 15 |
∴AE=9.
点评:此题考查了相似的判定以及垂径定理、勾股定理的应用,难易适中.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 已知:如图,两个以O为圆心的同心圆,AB是大圆的直径,弦BC切小圆于点D,CE⊥AB,垂足为E,大圆的直径为25,小圆的直径为15米.求AE的长.
已知:如图,两个以O为圆心的同心圆,AB是大圆的直径,弦BC切小圆于点D,CE⊥AB,垂足为E,大圆的直径为25,小圆的直径为15米.求AE的长.