题目内容
如下图，已知矩形ABCD的对角线AC、BD相交于O，OF⊥AD于F，OF＝3cm，AE⊥BD于E，且BE∶ED＝1∶3，求AC的长．
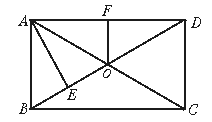
答案：12cm
解析：
提示：
解析：
|
∵四边形ABCD是矩形， ∴AC＝BD，OB＝OD＝OA＝OC 又∵BE∶ED＝1∶3 ∴BE∶BO＝1∶2 ∴BE＝EO 又∵AE⊥BO ∴△ABE≌△AOE ∴AB＝OA即AB＝AO＝OB ∴∠BAE＝∠EAO＝30°，∠FAO＝30° ∴△ABE≌△AOF ∴BE＝OF＝3 cm，∴BD＝12 cm ∴AC＝BD＝12 cm |
提示：
|
本题主要利用矩形的有关性质，进行计算．即：由矩形的对角线互相平分且相等；可导出BE＝OE，进而得出AB＝AO，进一步得出BE＝OF＝3 cm，求出BD的长，即可求得AC的长． |
练习册系列答案
名校课堂系列答案
相关题目
，顶点A所经过的路线长等于______．
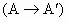)，顶点A所经过的路线长等于________．
