题目内容
【题目】如图,四边形ABCD与四边形OEFG都是正方形,O是正方形ABCD的中心,OE交BC于点M,OG交CD于点N,下列结论:①△ODG≌△OCE;②GD=CE;③OG⊥CE;④若正方形ABCD的边长为2,则四边形OMCN的面积等于1,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据O是正方形ABCD的中心以及四边形OEFG是正方形,利用SAS可证明△DOG≌△COE,根据全等三角形的性质可得DG=CE,由此可判定①②正确,由正方形OEFG可得OE⊥OG,从而可得OG不垂直CE,判定③错误,证明△DON≌△COM,从而可得S△DON=S△COM,继而根据正方形面积公式可求得S四边形OMCN=S△COD=1,判定④正确,据此即可得答案.
∵O是正方形ABCD的中心,
∴OD=OC,AC⊥BD,∠ODN=∠OCM=45°,
∴∠DOC=90°,
∵四边形OEFG是正方形,
∴OG=OE,∠EOG=90°,
∴∠DOG=∠COE,
在△DOG和△COE中,
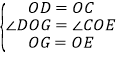 ,
,
∴△DOG≌△COE,
∴DG=CE,所以①②正确,
∵∠EOG=90°,
∴OE⊥OG,
过点E有且只有一条直线和OG垂直,
∴OG不垂直CE,所以③错误;
在△DON和△COM中,
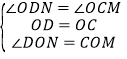 ,
,
∴△DON≌△COM,
∴S△DON=S△COM,
∴S四边形OMCN=S△COD,
∵正方形ABCD的边长为2,
∴S△COD=![]() S正方形ABCD=1,
S正方形ABCD=1,
∴S四边形OMCN=S△COD=1,所以④正确,
即:正确的有①②④,
故选C.

练习册系列答案
相关题目











