题目内容
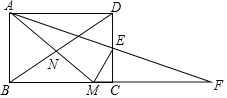
【题目】如图,在矩形ABCD中,![]() ,E为CD边的中点,将
,E为CD边的中点,将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,点D的对应点为C,点A的对应点为F,过点E作
,点D的对应点为C,点A的对应点为F,过点E作![]() 交BC于点M,连接AM、BD交于点N,现有下列结论:
交BC于点M,连接AM、BD交于点N,现有下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 点N为
点N为![]() 的外心.其中正确的个数为
的外心.其中正确的个数为![]()
![]()
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】分析:
(1)由旋转的性质易得AD=FC,AE=FE,结合ME⊥AF可得AM=MF,结合MF=MC+CF即可得到结论①成立;(2)假设AM=DE+BM成立,则结合(1)可推得CE=2MC,但由题中条件不能得到CE=2MC一定成立,故结论②不成立;(3)由已知条件证△ADE∽△ECM,结合DE=CE即可证得结论③成立;(4)过点M作MF⊥AD于点F,连接BF交AM于点Q,则易证点Q是AM的中点,由此可得点N不是AM的中点,从而可得结论④不成立;综合(1)--(4)即可得到所求答案.
详解:
(1)∵△CEF是由△DEA绕点E旋转180°得到的,
∴AD=FC,AE=FE,DE=CE,
又∵ME⊥AF,
∴AM=MF,
∵MF=MC+CF,
∴AM=AD+MC,即结论①成立;
(2)假设AM=DE+BM成立,
∵由(1)可知AM=AD+MC,
∴AD+MC=DE+BM,
又∵AD=BC=BM+MC,DE=CE,
∴BM+MC+MC=BM+CE,
∴2MC=CE,
∵由题中条件不能确定CE=2MC成立,
∴AM=DE+BM不一定成立,故结论②不成立;
(3)∵ME⊥AF,四边形ABCD是矩形,
∴∠ADE=∠MEF=∠ECM=90°,
∴∠MEC+∠EMC=90°,∠EMC+∠F=90°,
∴∠MEC=∠F,
∵AD∥BC,
∴∠DAE=∠F,
∴∠DAE=∠MEC,
∴△ADE∽△ECM,
∴AD:EC=DE:CM,
∴EC·DE=AD·CM,
又∵EC=DE,
∴DE2=AD·CM,故结论③成立;
(4)如下图,过点M作MF⊥AD于点F,连接BF交AM于点Q,
∴∠ABM=∠BAF=∠AFM=90°,
∴四边形ABMF是矩形,
∴点Q是AM的中点,
∴点Q是△ABM的外心,
∵点Q与点N不重合,
∴点N不是△ABM的外心,故结论④不成立.
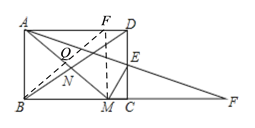
综上所述,上述4个结论中,成立的是①③,共2个.
故选B.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案