题目内容
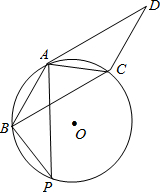 如图,平行四边形ABCD的对角线AC=AB,⊙O经过A、B、C三点.
如图,平行四边形ABCD的对角线AC=AB,⊙O经过A、B、C三点.(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若点P在优弧AB上,连接AP、BP,且BC=8cm,AB=5cm,求∠APB的正弦值.
分析:(1)连接OA根据垂径定理得出OA⊥BC,推出OA⊥AD,根据切线的判定推出即可;
(2)求出BE和EC,求出∠APB=∠ACE,根据锐角三角函数的定义求出即可.
(2)求出BE和EC,求出∠APB=∠ACE,根据锐角三角函数的定义求出即可.
解答:(1)解:直线AD与⊙O的位置关系是相切,
理由是:连接OA交BC于E,
∵AB=AC,
∴弧AB=弧AC,
∴AO⊥BC,BE=EC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴OA⊥AD,
∵OA是半径,
∴直线AD是⊙O的切线;
(2)∵BC=8,
∴BE=EC=4,
∵AB=AC=5,
∴由勾股定理得:AE=3,
∵弧AB=弧AC,
∴∠APB=∠ACE,
则tan∠APB=tan∠ACE=
=
.
理由是:连接OA交BC于E,

∵AB=AC,
∴弧AB=弧AC,
∴AO⊥BC,BE=EC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴OA⊥AD,
∵OA是半径,
∴直线AD是⊙O的切线;
(2)∵BC=8,
∴BE=EC=4,
∵AB=AC=5,
∴由勾股定理得:AE=3,
∵弧AB=弧AC,
∴∠APB=∠ACE,
则tan∠APB=tan∠ACE=
| AE |
| CE |
| 3 |
| 4 |
点评:本题考查了切线的判定,垂径定理,平行四边形的性质,勾股定理的应用,主要考查学生的推理能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB. 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是

 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为