题目内容
当x依次取1,2,3,…,2009,| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| x2 |
| 1+x2 |
分析:因为当x=
时和当x=k时,分别代入代数式
,再把它们所得的和相加的1.2,3,…,2009,
,
,
,…,
恰好分别对应互为相反数,从而问题的得解.
| 1 |
| k |
| x2 |
| 1+x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
解答:解:∵当x=
时,
=
,
当x=k时,
=
,
故这两值相加得:
+
=1,
∴当x依次取1,2,3,…2009,
,
,
,…,
时,
原式=
+
+
+…+
+
+
+…+
,
=
+(
+
)+(
+
)+…+(
+
),
=
+1+1+…1,
=2008
.
| 1 |
| k |
| x2 |
| 1+x2 |
| 1 |
| 1+k2 |
当x=k时,
| x2 |
| 1+x2 |
| k 2 |
| 1+k2 |
故这两值相加得:
| 1 |
| 1+k 2 |
| k 2 |
| 1+k2 |
∴当x依次取1,2,3,…2009,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
原式=
| 1 |
| 2 |
| 4 |
| 5 |
| 9 |
| 10 |
| 2009 2 |
| 1+2009 2 |
| 1 |
| 5 |
| 1 |
| 10 |
| ||
1+
|
=
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 9 |
| 10 |
| 1 |
| 10 |
| 2009 2 |
| 1+2009 2 |
| ||
1+
|
=
| 1 |
| 2 |
=2008
| 1 |
| 2 |
点评:本题考查因式分解在分式化简中的运用,在化简中注意不同的分式相加是一个常数.

练习册系列答案
相关题目
 ,
, ,
,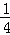 ,…,
,…, 时,代数式
时,代数式 的值的和等于 .
的值的和等于 . ,
, ,
, ,…,
,…,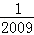 时,代数式
时,代数式 的值的和等于 .
的值的和等于 . ,
, ,
, ,…,
,…, 时,代数式
时,代数式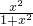 的值的和等于________.
的值的和等于________.