Question

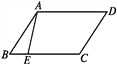
【题目】如图①，是用3根相同火柴棒拼成的一个三角图形，记为一个基本图形，将此基本图形不断的复制，使得相邻的两个基本图形的边重合，这样得到图②，图③…

（1）观察以上图形，图④中所用火柴棒的根数为_________，

猜想：在图n中，所用火柴棒的根数为_________（用n表示）；

（2）如图，将图n放在直角坐标系中，设其中第一个基本图形的中心O1的坐标为（，），则=_________；的坐标为_________.

Answer 1

【答案】(1)9, 2n+1;（2）1；（2014，2）.

【解析】

（1）按照图中火柴的个数填表即可当三角形的个数为：1、2、3、4时，火柴棒的个数分别为：3、5、7、9，由此可以看出当三角形的个数为n时，三角形个数增加n-1个，那么此时火柴棒的个数应该为：3+2（n-1）=2n+1，得出答案；

（2）如图，作O1A⊥x轴，连接OO1，由等边三角形的性质以及勾股定理可求得y1=1，从而可得O1的坐标为（，1），继而求得O2的坐标为（2，2），同理可得O3的坐标为（3，1），O4的坐标为（4，2），由此发现规律即可得O2014的坐标为（2014，2）．

（1）观察以上图形，图④中所用火柴棒的根数为9，

猜想：在图n中，所用火柴棒的根数为2n+1（用n表示），

故答案为9，2n+1；

（2）将图n放在直角坐标系中，其中第一个基本图形的中心的坐标为（，)，

如图，作O1A⊥x轴，连接OO1，则有AO=，∠AOO1=30°，

∴OO1=2O1A，

又OA2+O1A2=O1O2，

∴OO1=2，O1A=1，

∴y1=1，

∴的坐标为（，1)，

按图示的辅助线，可得O1B=O1C=O1A=2，OC=2OA=2，O2C=2，

∴的坐标为（2，2），

同理，的坐标为（3，1），的坐标为（4，2），

…，

∴的坐标为（2014，2），

故答案为： 1；（2014，2）.