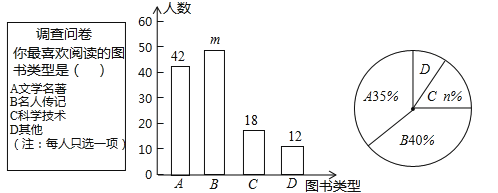
��Ŀ����
����Ŀ����֪������ABCD�У���MAN=45������MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N.����MAN�Ƶ�A��ת��BM=DNʱ����ͼ1������֤BM��DN��MN��
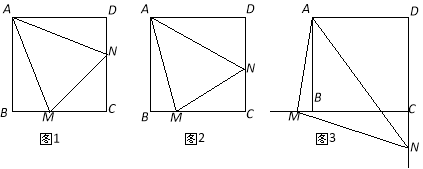
��1������MAN�Ƶ�A��ת��BM��DNʱ����ͼ2�����߶�BM��DN��MN֮����������������ϵ?д�����룬������֤����
��2������MAN�Ƶ�A��ת����ͼ3��λ��ʱ���߶�BM��DN��MN֮������������������ϵ����д����IJ��벢����֤����
���𰸡���1����BM��DN=MN������֤�����̼���������2����DN��BM��MN��֤�����̼�����.
��������
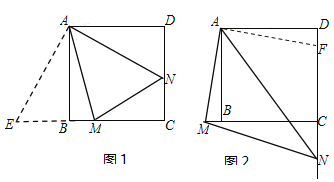
�����������1������MB���ӳ����ϣ��ص�BE=DN������AE�õ���ABE�ա�AND���Ӷ��õ�AE=AN��Ȼ��֤����AEM�ա�ANM���õ�ME=MN���Ӷ��ó��𰸣���2������DC�Ͻ�ȡDF=BM������AF�õ���ABM�ա�ADF��Ȼ��֤����MAN�ա�FAN���õ�����Ĵ�.
�����������1����BM��DN=MN������
����ͼ1����MB���ӳ����ϣ��ص�BE=DN������AE����֤����ABE�ա�AND����AE=AN��
���EAB=��NMD�����BAD=90��,��NAM=45��
���BAM+��NMD=45�������EAB+��BAM=45�������EAM=��NAM![]() ��AMΪ�����ߣ����AEM�ա�ANM ��
��AMΪ�����ߣ����AEM�ա�ANM ��
��ME=MN����ME=BE��BM=DN��BM.��DN+BM=MN.
��2����DN��BM��MN��
��ͼ2����DC�Ͻ�ȡDF=BM������AF����AB=AD����ABM=��ADF=90�������ABM�ա�ADF ��SAS��
��AM=AF����MAB=��FAD�����MAB+��BAF=��FAD+��BAF=90��������MAF=��BAD=90����
����MAN=45�������NAF=��MAN=45������AN=AN�����MAN�ա�FAN����MN=FN���� MN=DN��DF=DN��BM��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�