Question

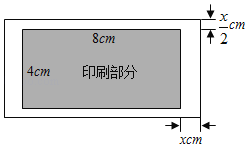
【题目】如图，印刷一张矩形的包装纸，印刷部分的长为8cm，宽为4cm，上下空白宽各cm，左右空白宽各xcm，四周空白处的面积为Scm2．

（1）求S与x的关系式；

（2）当四周空白处的面积为18cm2时，求x的值．

Answer 1

【答案】（1）S＝2x2+16x；（2）所以当四周空白处的面积为18cm2时，x的值为1

【解析】

（1）矩形的总面积＝印刷面积32+空白部分面积S，据此列出函数关系式即可．

（2）令S等于18即可求得到关于x的一元二次方程，进而就能求出这张广告的纸张的长和宽．

解：（1）因为印刷部分的面积是4×8＝32cm2，上下空白宽各m，左右空白宽各xcm，

则S+32＝(8+2x)(x+4)；

∴S＝2x2+16x；

（2）根据题意有2x2+16x＝18．

整理得x2+8x﹣9＝0，

解得x＝1或x＝﹣9（舍去），

所以当四周空白处的面积为18cm2时，x的值为1．