Question

在平面直角坐标系中，已知点A（4，0），点B（0，3），点P从点A出发，以每秒1个单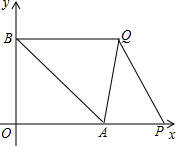位的速度在x轴上向右平移，点Q从B点出发，以每秒2个单位的速度沿直线y=3向右平移，又P、Q两点同时出发，设运动时间为t秒．
（1）当t为何值时，四边形OBPQ的面积为8；
（2）连接AQ，当△APQ是直角三角形时，求Q的坐标．

Answer 1

分析：（1）设运动时间为t秒，BQ=2t，OQ=4+t，根据梯形面积公式，求出t；
（2）要分∠QAP为直角和∠QPA和∠AQP为直角，分别求出Q点坐标．

解答：解：（1）设运动时间为t秒，BQ=2t，OQ=4+t，
s=

1

2

（3t+4）×3=8
解得t=

4

9

；

（2）当∠QAP=90°时，Q（4，3）；
当∠QPA=90°时，Q（8，3）；
当∠AQP=90°时，不存在Q点的坐标，
故Q点坐标为（4，3）、（8，3）．

点评：本题主要考查翻折变换的折叠问题，还涉及坐标与图形性质等知识点．