Question

【题目】如图,根据图中信息解答下列问题:

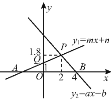
(1)关于x的不等式ax+b>0的解集是　　.

(2)关于x的不等式mx+n<1的解集是　　.

(3)当x为何值时,y1≤y2?

(4)当x为何值时,0<y2<y1?

Answer 1

【答案】:(1) x<4;(2) x<0;(3)x≤2;(4)2<x<4.

【解析】

（1）求ax+b＞0的解集，只需确定直线y2在x轴上方时x的取值范围即可；

（2）求mx+n＜1的解集，也就是求直线y1在y=1下方时x的取值范围，据此解答即可；
（3）找出直线y1在直线y2的下方与相交时x的取值范围，据此可确定y1≤y2时x的取值范围；
（4）根据函数图象，找出直线y2在直线y1的下方且在x轴上方时x的取值范围即可.

(1)∵直线y2=ax+b与x轴的交点是(4,0),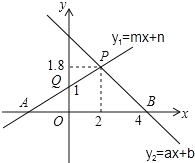

∴当x<4时, y2>0，即不等式ax+b>0的解集是x<4；

(2)∵直线y1=mx+n与y轴的交点是(0,1)，

∴当x<0时, y1<1，即不等式mx+n<1的解集是x<0；。

(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时，有x2，

所以当x2时, y1 y2；

(4)如图所示,当2<x<4时,0< y2< y1.

故答案为：(1) x<4; (2) x<0; (3)x≤2; (4)2<x<4.