题目内容
如图，△ABC的面积为18cm2，点D、E、F分别位于AB、BC、CA上．且AD=4cm，DB=5cm．如果△ABE的面积和四边形DBEF的面积相等，则△ABE的面积是
- A.8cm2
- B.9cm2
- C.10cm2
- D.12cm2
C
分析：本题由题意可知△ABE的面积和四边形DBEF的面积相等，可通过连接DE，DC的方法，证明出DE∥AC，进而求出△BDC的面积，然后即可求出答案．
解答：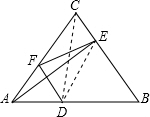
解：连接DE，DC．
∵SDBEF=S△ABE
∴S△ADE=S△FDE，
∵两个三角形有公共底DE，且面积相等，
∴高相等，
∴DE∥AC
从而可得：S△ADE=S△CDE
∴S△ABE=S△BDC
又AD=4，DB=5∴
=10cm2
即S△ABE=10cm2
故应选：C．
点评：本题考查三角形面积性质的应用，可通过作辅助线的方法，做此题时注意理清各个三角形面积之间的关系．
分析：本题由题意可知△ABE的面积和四边形DBEF的面积相等，可通过连接DE，DC的方法，证明出DE∥AC，进而求出△BDC的面积，然后即可求出答案．
解答：
解：连接DE，DC．∵SDBEF=S△ABE
∴S△ADE=S△FDE，
∵两个三角形有公共底DE，且面积相等，
∴高相等，
∴DE∥AC
从而可得：S△ADE=S△CDE
∴S△ABE=S△BDC
又AD=4，DB=5∴
=10cm2即S△ABE=10cm2
故应选：C．
点评：本题考查三角形面积性质的应用，可通过作辅助线的方法，做此题时注意理清各个三角形面积之间的关系．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
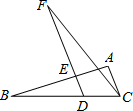如图，△ABC的面积是63，D是BC上的一点，且BD：CD=2：1，DE∥AC交AB于E，延长DE到F，使FE：ED=2：1，则△CDF的面积是
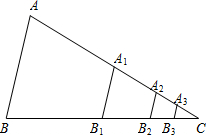如图，△ABC的面积为1，分别取AC、BC两边的中点A1、B1，则四边形A1ABB1的面积为
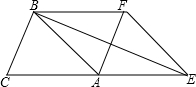如图，△ABC的面积为
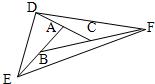3、如图，△ABC的面积为1，若把△ABC的各边分别延长一倍，得到一个新的△DEF，则S△DEF=
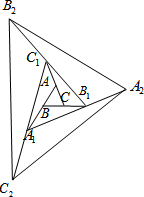如图，△ABC的面积为1．第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连结A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连结A2，B2，C2，得到△A2B2C2．…按此规律，要使得到的三角形的面积超过2013，最少经过