题目内容
 如图,△ABC的面积为
如图,△ABC的面积为| 2 |
(1)试判断四边形BAEF的形状,并说明理由;
(2)若∠BEC=22.5°,求AC的长.
分析:(1)由平移可得到∠BAC=∠FEA,AE=AC=AB=EF,那么四边形BAEF是平行四边形,由邻边相等可得到是菱形;
(2)由菱形的邻边相等可得角相等,易得∠BAC=45°,作出AC边上的高,则高及AB所在三角形是等腰直角三角形,设所求边为未知数,用它表示出高,利用已给面积即可求解.
(2)由菱形的邻边相等可得角相等,易得∠BAC=45°,作出AC边上的高,则高及AB所在三角形是等腰直角三角形,设所求边为未知数,用它表示出高,利用已给面积即可求解.
解答:解:(1)菱形.(2分)
证明:由题意得:AB=EF,∠BAC=∠FEA,CA=AE,
∴AB∥EF.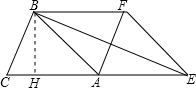
∴四边形BAEF是平行四边形.
∵AB=AC,
∴AB=AE,
∴四边形BAEF是菱形.(3分)
(2)作BH⊥AC于H,
∠BAC=2∠BEC=45°,
AB=AC=
BH,S△ABC=
AC•BH=
,
AC=2.(5分)
证明:由题意得:AB=EF,∠BAC=∠FEA,CA=AE,
∴AB∥EF.

∴四边形BAEF是平行四边形.
∵AB=AC,
∴AB=AE,
∴四边形BAEF是菱形.(3分)
(2)作BH⊥AC于H,
∠BAC=2∠BEC=45°,
AB=AC=
| 2 |
| 1 |
| 2 |
| 2 |
AC=2.(5分)
点评:平移前后对应线段,对应角相等,作高构造特殊直角三角形是常用的辅助线作法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是
如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为 3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF=
3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF= 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过