题目内容
Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .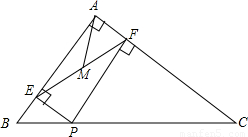
【答案】分析:AM= EF=
EF= AP,所以当AP最小时,AM最小,根据垂线段最短解答.
AP,所以当AP最小时,AM最小,根据垂线段最短解答.
解答:解:由题意知,四边形AFPE是矩形,
∵点M是矩形对角线EF的中点,则延长AM应过点P,
∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,
此时AM= AP,由勾股定理知BC=
AP,由勾股定理知BC=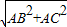 =5,
=5,
∵S△ABC= AB•AC=
AB•AC= BC•AP,
BC•AP,
∴AP=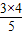 =
=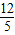 ,
,
∴AM= AP=
AP= .
.
点评:本题利用了矩形的性质、勾股定理、垂线段最短求解.
 EF=
EF= AP,所以当AP最小时,AM最小,根据垂线段最短解答.
AP,所以当AP最小时,AM最小,根据垂线段最短解答.解答:解:由题意知,四边形AFPE是矩形,
∵点M是矩形对角线EF的中点,则延长AM应过点P,
∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,
此时AM=
 AP,由勾股定理知BC=
AP,由勾股定理知BC=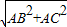 =5,
=5,∵S△ABC=
 AB•AC=
AB•AC= BC•AP,
BC•AP,∴AP=
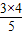 =
=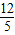 ,
,∴AM=
 AP=
AP= .
.点评:本题利用了矩形的性质、勾股定理、垂线段最短求解.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
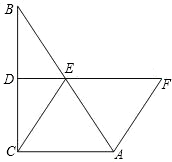 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=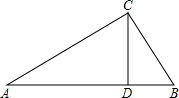 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=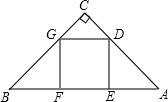 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为