题目内容
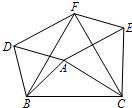 18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
18、如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足
∠BAC=150°
条件时,四边形DAEF是矩形;②当△ABC满足
AB=AC≠BC
条件时,四边形DAEF是菱形;③当△ABC满足
∠BAC=60°
条件时,以D、A、E、F为顶点的四边形不存在.分析:(1)、根据等边三角形的性质证△ABC≌△DBF≌△EFC,就有AD=EF,DF=CE,从而得证四边形DAEF是平行四边形;
(2)、当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,所以平行四边形DAEF是矩形;
当AB=AC≠BC,有AD=AE,所以平行四边形DAEF是菱形;
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
(2)、当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,所以平行四边形DAEF是矩形;
当AB=AC≠BC,有AD=AE,所以平行四边形DAEF是菱形;
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
解答:证明:(1)∵△ABD和△FBC都是等边三角形,
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA-∠FBA=∠FBC-∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中
BD=BA,∠DBF=∠ABC,BF=BC,
∴△ABC≌△DBF.(2分)
∴AC=DF=AE.(3分)
同理△ABC≌△EFC.
∴AB=EF=AD.(4分)
∴四边形ADFE是平行四边形.(6分)
(2)当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,
∴平行四边形DAEF是矩形.
当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA-∠FBA=∠FBC-∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中
BD=BA,∠DBF=∠ABC,BF=BC,
∴△ABC≌△DBF.(2分)
∴AC=DF=AE.(3分)
同理△ABC≌△EFC.
∴AB=EF=AD.(4分)
∴四边形ADFE是平行四边形.(6分)
(2)当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,
∴平行四边形DAEF是矩形.
当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为顶点的四边形不存在.
点评:本题利用了等边三角形的性质和全等三角形的判定和性质.

练习册系列答案
相关题目
 如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.
如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.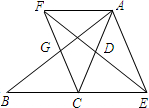 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF. 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=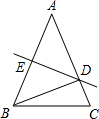 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为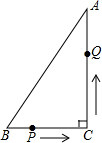 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.