题目内容
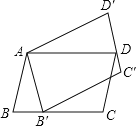
【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.

(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
【答案】(1)略;(2)菱形BFDE的面积为:![]()
【解析】试题分析:(1)、根据矩形的性质可得∠ABD=∠CDB,根据折叠可得∠EBD=∠FDB,则BE∥DF,根据两组对边分别平行的四边形为平行四边形进行证明;(2)、根据菱形可得BE=DE,有折叠可得BM=AB=2,则DM=BM=2,BD=4,根据勾股定理可得AD=2![]() ,设DE=x,则AE=2
,设DE=x,则AE=2![]() -x,BE=x,根据Rt△ABE的勾股定理得出x的值,然后计算菱形的面积.
-x,BE=x,根据Rt△ABE的勾股定理得出x的值,然后计算菱形的面积.
试题解析:(1)、∵四边形ABCD是矩形 ∴ AB∥CD AD∥BC ∴∠ABD=∠CDB
由折叠知:∠EBD=∠ABD,∠FDB=∠CDB ∴∠EBD=∠FDB ∴BE//DF
∴四边形BFDE是平行四边形
(2)、∵四边形BFDE是菱形 ∴ BE=DE 由折叠知:∠EMB=∠A=90°BM=AB=2
∴DM=BM=2 ∴BD=4 由勾股定理解得AD=2![]() 设DE=x,则AE=2
设DE=x,则AE=2![]() ―x,BE=x
―x,BE=x
在Rt△ABE中,AE2+AB2=BE2 (2![]() ―x)2+22=x2 解得:x=
―x)2+22=x2 解得:x=![]()
∴菱形BFDE的面积为![]() ×2=
×2=![]()

练习册系列答案
相关题目