题目内容
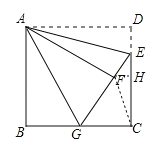
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )

A.2 B.3 C.4 D.5
【答案】D.
【解析】
试题分析:∵正方形ABCD的边长为6,CE=2DE,∴DE=2,EC=4,∵把△ADE沿AE折叠使△ADE落在△AFE的位置,∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,在Rt△ABG和Rt△AFG中,∵AB=AF,AG=AG,∴Rt△ABG≌Rt△AFG(HL),∴GB=GF,∠BAG=∠FAG,∴∠GAE=∠FAE+∠FAG=![]() ∠BAD=45°,所以①正确;
∠BAD=45°,所以①正确;
设BG=x,则GF=x,C=BC﹣BG=6﹣x,在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,∵![]() ,∴
,∴![]() ,解得x=3,∴BG=3,CG=6﹣3=3,∴BG=CG,所以②正确;
,解得x=3,∴BG=3,CG=6﹣3=3,∴BG=CG,所以②正确;
∵EF=ED,GB=GF,∴GE=GF+EF=BG+DE,所以③正确;
∵GF=GC,∴∠GFC=∠GCF,又∵Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF,而∠BGF=∠GFC+∠GCF,∴∠AGB+∠AGF=∠GFC+∠GCF,∴∠AGB=∠GCF,∴CF∥AG,所以④正确;
过F作FH⊥DC.∵BC⊥DH,∴FH∥GC,∴△EFH∽△EGC,∴![]() ,EF=DE=2,GF=3,∴EG=5,∴△EFH∽△EGC,∴相似比为:
,EF=DE=2,GF=3,∴EG=5,∴△EFH∽△EGC,∴相似比为:![]() =
=![]() ,∴S△FGC=S△GCE﹣S△FEC=
,∴S△FGC=S△GCE﹣S△FEC=![]() ×3×4﹣
×3×4﹣![]() ×4×(
×4×(![]() ×3)=3.6,所以⑤正确.
×3)=3.6,所以⑤正确.
故正确的有①②③④⑤,故选D.

练习册系列答案
相关题目