题目内容
先阅读下列第(1)题的解答过程:(1)已知a,β是方程x2+2x-7=0的两个实数根,求a2+3β2+4β的值.
解法1:∵a,β是方程x2+2x-7=0的两个实数根,
∴a2+2a-7=0,β2+2β-7=0,且a+β=-2.
∴a2=7-2a,β2=7-2β.
∴a2+3β2+4β=7-2a+3(7-2β)+4β=28-2(a+β)=28-2×(-2)=32.
解法2:由求根公式得a=1+2
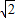 ,β=-1-2
,β=-1-2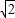 .
.∴a2+3β2+4β=(-1+2
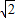 )2+3(-1-2
)2+3(-1-2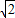 )2+4(-1-2
)2+4(-1-2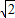 )
)=9-4
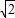 +3(9+4
+3(9+4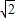 )-4-8
)-4-8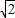 =32.
=32.当a=-1-2
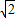 ,β=-1+2
,β=-1+2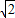 时,同理可得a2+3β2+4β=32.
时,同理可得a2+3β2+4β=32.解法3:由已知得a+β=-2,aβ=-7.
∴a2+β2=(a+β)2-2aβ=18.
令a2+3β2+4β=A,β2+3a2+4a=B.
∴A+B=4(a2+β2)+4(a+β)=4×18+4×(-2)=64.①
A-B=2(β2-a2)+4(β-a)=2(β+a)(β-a)+4(β-a)=0.②
①+②,得2A=64,∴A=32.
请仿照上面的解法中的一种或自己另外寻注一种方法解答下面的问题:
(2)已知x1,x2是方程x2-x-9=0的两个实数根,求代数式x13+7x22+3x2-66的值.
【答案】分析:首先利用根与系数的关系得到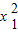 =x1+9,
=x1+9,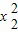 =x2+9,然后将原式变形为x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.
=x2+9,然后将原式变形为x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.
解答:解∵x1,x2是方程x2-x-9=0的两个实数根,
∴x1+x2=1,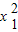 -x1-9=0,
-x1-9=0,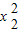 -x2-9=0,
-x2-9=0,
即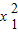 =x1+9,
=x1+9,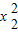 =x2+9.
=x2+9.
∴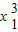 +7
+7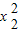 +3x2-66
+3x2-66
=x1(x1+9)+7(x2+9)+3x2-66
=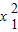 +9x1+10x2-3
+9x1+10x2-3
=x1+9+9x1+10x2-3
=10(x1+x2)+6
=16.?
点评:本题是一道阅读理解题,考查一元二次方程根的不对称式值的求解.解法1应用一元二次方程根的定义,根与系数的关系和逐步降次的方法求解;解法2应用求根公式法求出方程的解,再直接代入待求式求值;解法3通过构造与待求式对称的对偶式,结合根与系数的关系求解,求不对称式的值源自于中学竞赛内容,知识点略高于中考要求,故题中提供了可借鉴的三种解法,不仅降低了问题难度,而且侧重考查了自学能力,吻合了素质教育对学生自学能力培养的要求.解答这类题,透彻理解阅读材料,并灵活选用合理方法加以运用是前提.第(2)问题选用解法1的方法较为简便.
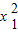 =x1+9,
=x1+9,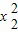 =x2+9,然后将原式变形为x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.
=x2+9,然后将原式变形为x1(x1+9)+7(x2+9)+3x2-66,整理后代入即可求值.解答:解∵x1,x2是方程x2-x-9=0的两个实数根,
∴x1+x2=1,
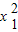 -x1-9=0,
-x1-9=0,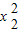 -x2-9=0,
-x2-9=0,即
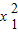 =x1+9,
=x1+9,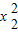 =x2+9.
=x2+9.∴
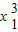 +7
+7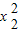 +3x2-66
+3x2-66=x1(x1+9)+7(x2+9)+3x2-66
=
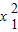 +9x1+10x2-3
+9x1+10x2-3=x1+9+9x1+10x2-3
=10(x1+x2)+6
=16.?
点评:本题是一道阅读理解题,考查一元二次方程根的不对称式值的求解.解法1应用一元二次方程根的定义,根与系数的关系和逐步降次的方法求解;解法2应用求根公式法求出方程的解,再直接代入待求式求值;解法3通过构造与待求式对称的对偶式,结合根与系数的关系求解,求不对称式的值源自于中学竞赛内容,知识点略高于中考要求,故题中提供了可借鉴的三种解法,不仅降低了问题难度,而且侧重考查了自学能力,吻合了素质教育对学生自学能力培养的要求.解答这类题,透彻理解阅读材料,并灵活选用合理方法加以运用是前提.第(2)问题选用解法1的方法较为简便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,β=-1-2
,β=-1-2