题目内容
先阅读下列第(1)题的解答过程,再解第(2)题.
(1)已知实数a、b满足a2=2-2a,b2=2-2b,且a≠b,求
+
的值.
由已知得:a2+2a-2=0,b2+2b-2=0,且a≠b,故a、b是方程:x2+2x-2=0的两个不相等的实数根,由根与系数的关系得:a+b=-2,ab=-2.
∴
+
=
=4.
(2)已知p2-2p-5=0,5q2+2q-1=0,其中p、q为实数,求p2+
的值.
(1)已知实数a、b满足a2=2-2a,b2=2-2b,且a≠b,求
| a |
| b |
| b |
| a |
由已知得:a2+2a-2=0,b2+2b-2=0,且a≠b,故a、b是方程:x2+2x-2=0的两个不相等的实数根,由根与系数的关系得:a+b=-2,ab=-2.
∴
| a |
| b |
| b |
| a |
| (a+b)2-2ab |
| ab |
(2)已知p2-2p-5=0,5q2+2q-1=0,其中p、q为实数,求p2+
| 1 |
| q2 |
由5q2+2q-1=0两边同除以-q2,得:
-
-5=0,而p2-2p-5=0,
故p和
是方程x2-2x-5=0的两根,
由根与系数的关系得:p+
=2,p•
=-5,
所以p2+
=(p+
)2-2×
=14.
| 1 |
| q2 |
| 2 |
| q |
故p和
| 1 |
| q |
由根与系数的关系得:p+
| 1 |
| q |
| 1 |
| q |
所以p2+
| 1 |
| q2 |
| 1 |
| q |
| p |
| q |

练习册系列答案
相关题目
 ,β=-1-2
,β=-1-2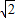 ,β=-1-2
,β=-1-2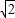 .
.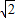 )2+3(-1-2
)2+3(-1-2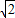 )2+4(-1-2
)2+4(-1-2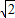 )
)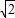 +3(9+4
+3(9+4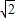 )-4-8
)-4-8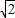 =32.
=32.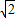 ,β=-1+2
,β=-1+2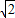 时,同理可得a2+3β2+4β=32.
时,同理可得a2+3β2+4β=32.