Question

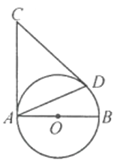
【题目】如图，CA，CD是⊙O的两条切线，切点分别为A，D，AB是⊙O的直径．

⑴ 若∠C＝50°，求∠BAD的度数；

⑵ 若AB＝AC＝4，求AD的长．

Answer 1

【答案】(1)25°;(2) .

【解析】

（1）连接OD，根据四边形内角和定理求得∠AOD，从而得出∠BOD的度数，根据∠BAD＝得出所求;

(2)先根据SAS证明△ACM≌△DCM得出∠CMA＝∠CMD＝90o，再根据AAS证明△ACM≌△BAD，得出AM＝DM＝BD，设BD＝x，则AD＝2x，在△ABD中，+=，解方程从而得到AD的长度.

(1)如图所示，连接OD，

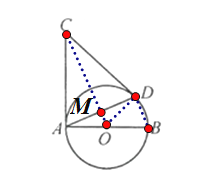
∵CA，CD是⊙O的两条切线，

∴∠OAC＝ODC＝90o，

又∵∠C＝50°，

∴四边形OACD中，∠AOD＝（360－90－90－50）°＝130°，

∴∠BOD＝50°，

∴∠BAD＝；

（2）∵CA，CD是⊙O的两条切线，

∴AC＝DC，∠ACO＝∠DCO，

在△ACM和△DCM中

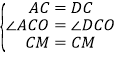
∴△ACM≌△DCM（SAS）

∴∠CMA＝∠CMD，AM＝DM

∴∠CMA＝∠CMD＝90o，

∵AB是⊙O的直径

∴∠ADB＝∠CMA，

∵∠BAD+∠MAC＝90o，∠BAD+∠DBA＝90o

∴∠DBA＝∠MAC

在△ACM和△BAD中

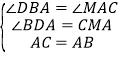
∴△ACM≌△BAD，

∴BD＝AM

又∵AM＝DM

∴AM＝DM＝BD

设BD＝x，则AD＝2x，在△ABD中，+=，

∴x=，

∴AD＝．