Question

【题目】已知，如图，是的直径，点为上一点，于点，交于点，与交于点，点为的延长线上一点，且.

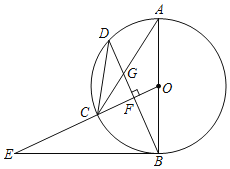
（1）求证：是的切线；

（2）求证：；

（3）若⊙O的半径为，的长为，求.

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

（1）由∠OEB=∠ACD，∠ACD=∠ABD知∠OEB=∠ABD，由OF⊥BD知∠BFE=90°，即∠OEB+∠EBF=90°，从而得∠ABD+∠EBF=90°，据此即可得证；
（2）连接AD，证△DCG∽△ACD即可得；
（3）先证△CDF∽△GCF得，再证△DCG∽△ABG得，据此知，由，，知AB=2r=5，根据,可得答案．

（1）证明：

∵，，

∴，

∵，

∴，

∴，

∴，

即，

∴，

∴是的切线；

（2）证明：连接，如图所示：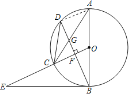

∵，

∴，

∴，

∵，

∴，

∴，∴；

（3）∵，∴，

∵，

∴，

而，

∴△CDF∽△GCF，∴，

又∵，，

∴，∴，∴，

∵，，∴，

∴.