Question

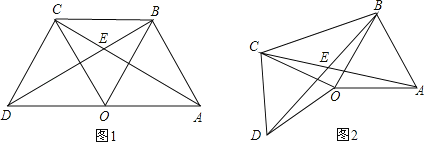
【题目】如图，点F在正方形ABCD的边BC上，E在AB的延长线上，FB＝EB，AF的延长线交CE于G，则∠AGC的度数是___________.

Answer 1

【答案】90°

【解析】

根据正方形的性质可得AB=CB，∠ABF=90°，从而求出∠ABF=∠CBE，然后利用SAS即可证出△ABF≌△CBE，从而证出∠BAF=∠BCE，然后利用直角三角形的两个锐角互余，即可证出∠BAF＋∠E=90°，最后利用三角形外角的性质即可求出∠AGC.

解：∵四边形ABCD是正方形

∴AB=CB，∠ABF=90°

∴∠CBE=180°－∠ABF=90°

∴∠ABF=∠CBE

在△ABF和△CBE中

∴△ABF≌△CBE

∴∠BAF=∠BCE

∵∠BCE＋∠E=90°

∴∠BAF＋∠E=90°

∴∠AGC=∠BAF＋∠E=90°

故答案为：90°.