题目内容
【题目】(2016·西宁中考)如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD.
(1)求证：CD是⊙O的切线；
(2)过点B作⊙O的切线交CD的延长线于点E，BC＝6， 
，求BE的长．
【答案】（1）见解析 （2）
(1)证明：连接OD.∵OB＝OD，∴∠OBD＝∠BDO.∵∠CDA＝∠CBD，∴∠CDA＝∠ODB.又∵AB是⊙O的直径，∴∠ADB＝90°，∴∠ADO＋∠ODB＝90°，∴∠ADO＋∠CDA＝90°，即∠CDO＝90°，∴OD⊥CD.∵OD是⊙O的半径，∴CD是⊙O的切线；
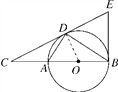
(2)解：∵∠C＝∠C，∠CDA＝∠CBD，∴△CDA∽△CBD，∴
＝
.∵＝
，BC＝6，∴CD＝4.∵CE，BE是⊙O的切线，∴BE＝DE，BE⊥BC，∴BE2＋BC2＝EC2，即BE2＋62＝(4＋BE)2，解得BE＝
.
【解析】试题分析：连接OD.根据圆周角定理得到∠ADO＋∠ODB＝90°，
而∠CDA＝∠CBD，∠CBD＝∠BDO.于是∠ADO＋∠CDA＝90°，可以证明是切线.
根据已知条件得到
由相似三角形的性质得到
求得
由切线的性质得到
根据勾股定理列方程即可得到结论．
试题解析：(1)连接OD.
∵OB＝OD，
∴∠OBD＝∠BDO.
∵∠CDA＝∠CBD，
∴∠CDA＝∠ODB.
又∵AB是⊙O的直径，∴∠ADB＝90°，
∴∠ADO＋∠ODB＝90°，
∴∠ADO＋∠CDA＝90°，即∠CDO＝90°，
∴OD⊥CD.
∵OD是⊙O的半径，
∴CD是⊙O的切线；
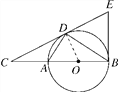
(2)∵∠C＝∠C，∠CDA＝∠CBD，∴△CDA∽△CBD，
BC＝6，∴CD＝4.
∵CE，BE是⊙O的切线，
∴BE＝DE，BE⊥BC，
∴BE2＋BC2＝EC2，
即BE2＋62＝(4＋BE)2，
解得BE＝
.
