题目内容
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
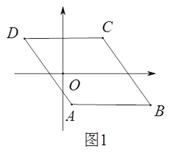

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
【答案】(1)点P的坐标为(3,4).(2)点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).(3)点P的坐标为(2,-4)或(![]() ,3)或(
,3)或(![]() ,4)或(
,4)或(![]() ,4).
,4).
【解析】试题(1)点P在BC上,要使PD=CD,只有P与C重合;
(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;
(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
试题解析:解:(1)∵CD=6,∴点P与点C重合,∴点P的坐标是(3,4).
(2)①当点P在边AD上时,由已知得,直线AD的函数表达式为:![]() ,设P(a,-2a-2),且-3≤a≤1.
,设P(a,-2a-2),且-3≤a≤1.
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,∴2a+2=a-1,解得a=-3,此时P(-3,4).
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,∴-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7.
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,∴4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,∴-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)因为直线AD为y=-2x-2,所以G(0,-2).
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,则可得M′P=PM=4+2=6,M′G=GM=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,解得m=-
,解得m=-![]() 或
或 ![]() ,则P( -
,则P( -![]() ,4)或(
,4)或( ![]() ,4);
,4);
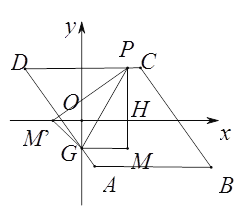
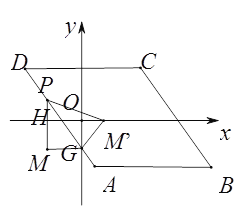
②如下图,当点P在AD边上时,设P(m,-2m-2),则PM′=PM=|-2m|,GM′=MG=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,整理得m= -
,整理得m= -![]() ,则P(-
,则P(-![]() ,3);
,3);
如下图,当点P在AB边上时,设P(m,-4),此时M′在y轴上,则四边形PM′GM是正方形,所以GM=PM=4-2=2,则P(2,-4).
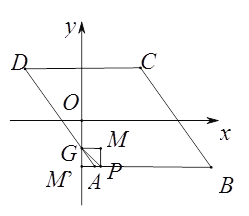
综上所述,点P的坐标为(2,-4)或(-![]() ,3)或(-
,3)或(-![]() ,4)或(
,4)或(![]() ,4).
,4).

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】 某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 | 销售数量(盏) | 销售收入(元) | |
A品牌 | B品牌 | ||
第一天 | 2 | 1 | 680 |
第二天 | 3 | 4 | 1670 |
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?