题目内容
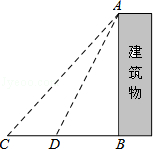
【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

【答案】(1)见解析;(2)25°
【解析】
(1)根据SAS即可证明;
(2)在△ABE中,求出∠A,∠ABE即可解决问题.
(1)证明:∵∠1=∠2,
∴∠1+∠EBF=∠2+∠EBF,
即∠ABE=∠CBF.
在△ABE和△CBF中,∵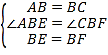
∴△ABE≌△CBF.
(2)∵∠1=∠2,∠FBE=40°,
∴∠1=∠2=70°.
∵△ABE≌△CBF,
∴∠A=∠C=45°,
∵∠ABE=∠1+∠FBE=70°+40°=110°,
∴∠E=180°-∠A-∠ABE=180°-45°-110°=25°.

练习册系列答案
相关题目
【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖 | 二等奖 | 三等奖 |
1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
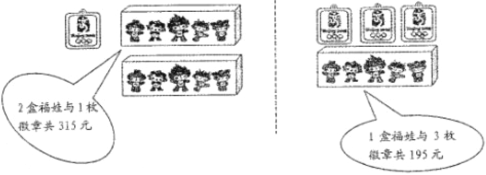
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?