题目内容
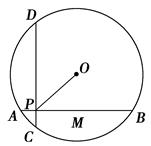
如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB＝CD＝8，则OP的长为 ( )
A．3 B．4
C．3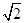
D．4
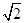
A．3 B．4
C．3
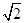D．4C
作OM⊥AB于M，ON⊥CD于N，连接OB，OD，
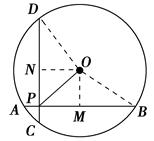
由垂径定理、勾股定理得：OM＝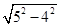
＝3，
∵弦AB、CD互相垂直，
∴∠DPB＝90°，
∵OM⊥AB于M，ON⊥CD于N，
∴∠OMP＝∠ONP＝90°
∴四边形MONP是正方形，∴OP＝3.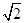
由垂径定理、勾股定理得：OM＝
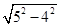＝3，∵弦AB、CD互相垂直，
∴∠DPB＝90°，
∵OM⊥AB于M，ON⊥CD于N，
∴∠OMP＝∠ONP＝90°
∴四边形MONP是正方形，∴OP＝3
.
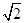练习册系列答案
学业测评一课一测系列答案
相关题目
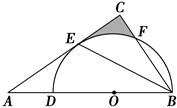
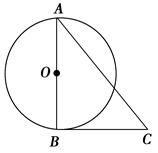
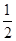，⊙O的半径为4，求图中阴影部分的面积．
上两点，且∠MEB=∠NFB=60°，则EM+FN= ．
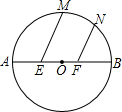
cm