题目内容
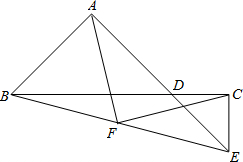
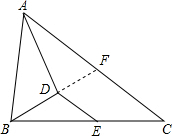
如图：△ABC中，AB=4，AC=6，AD平分∠BAC，BD⊥AD，E是BC中点，那么DE=______．
延长BD交AC于F点．
∵AD平分∠BAC，
∴∠FAD=∠BAD；
∵AD⊥BD，
∴∠ADF=∠ADB；
在△ADB和△ADF中
，
∴△ABD≌△AFD（ASA），
∴BD=DF，AF=AB=4．
∵AC=6，
∴FC=6-4=2，
∵E为BC中点，
∴BE=CE，
∴DE=
FC，
∴DE=1．
故答案为1．
∵AD平分∠BAC，
∴∠FAD=∠BAD；
∵AD⊥BD，
∴∠ADF=∠ADB；
在△ADB和△ADF中
|
∴△ABD≌△AFD（ASA），
∴BD=DF，AF=AB=4．
∵AC=6，
∴FC=6-4=2，
∵E为BC中点，
∴BE=CE，
∴DE=
| 1 |
| 2 |
∴DE=1．
故答案为1．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
