题目内容
 如下图所示,正方形A1B1C1D1、正方形A2B2C2D2,正方形A3B3C3D3、…,正方形AnBnCnDn均位于第一象限内,它们的边平行于x轴或y轴,其中点A1,A2,…,An在直线y=x上,点C1,C2,…,Cn在直线y=2x上.
如下图所示,正方形A1B1C1D1、正方形A2B2C2D2,正方形A3B3C3D3、…,正方形AnBnCnDn均位于第一象限内,它们的边平行于x轴或y轴,其中点A1,A2,…,An在直线y=x上,点C1,C2,…,Cn在直线y=2x上.结论1:若正方形A1B1C1D1的边长为1,则点B1坐标为(2,3);
结论2:若正方形A2B2C2D2的边长为2,则点B2坐标为(4,6);
结论3:若正方形A3B3C3D3的边长为3,
则点B3坐标为(6,9);
…
(1)请观察上面结论的规律,猜想出结论n(n是正整数);
(2)证明你猜想的结论n是正确的.
分析:(1)根据B1(2,3),B2(4,6),B3(6,9),…,可知B点横坐标为连续偶数,纵坐标为3的倍数;
(2)由于正方形AnBnCnDn的边长为n,因为An在直线y=x上,设An(a,a)则Bn(a-n,a),Cn(a-n,a+n),而Cn在直线y=2x上,代入求a、n的关系即可.
(2)由于正方形AnBnCnDn的边长为n,因为An在直线y=x上,设An(a,a)则Bn(a-n,a),Cn(a-n,a+n),而Cn在直线y=2x上,代入求a、n的关系即可.
解答:解:(1)由B1(2,3),B2(4,6),B3(6,9),…,猜想:Bn(2n,3n);
(2)依题意,AnBn=BnCn=n,
∵An在直线y=x上,设An(a,a)则Bn(a-n,a),Cn(a-n,a+n),
将Cn代入直线y=2x中,得a+n=2(a-n),解得a=3n,
∴a-n=2n,即Bn(2n,3n).
(2)依题意,AnBn=BnCn=n,
∵An在直线y=x上,设An(a,a)则Bn(a-n,a),Cn(a-n,a+n),
将Cn代入直线y=2x中,得a+n=2(a-n),解得a=3n,
∴a-n=2n,即Bn(2n,3n).
点评:本题考查了一次函数的综合运用.关键是由特殊到一般,猜想出一般结论,再根据正方形的性质,直线上点的坐标特点,设点的坐标,根据直线解析式求关系式,证明一般结论.

练习册系列答案
相关题目
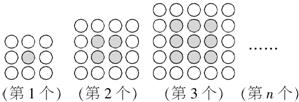
 (2007•西城区一模)玩具厂新出一套模板,它是由2个小正方形,5个大小不都全等的等腰直角三角形组成,拼成如下图所示的正方形.
(2007•西城区一模)玩具厂新出一套模板,它是由2个小正方形,5个大小不都全等的等腰直角三角形组成,拼成如下图所示的正方形. 在平面直角坐标系中,称横、纵坐标均为整数的点为整点,如下图所示的正方形内(包括边界)整点的个数是( )
在平面直角坐标系中,称横、纵坐标均为整数的点为整点,如下图所示的正方形内(包括边界)整点的个数是( )