题目内容
在Rt△ABC中,∠C=90°,AB=5,BC=4,求内切圆半径________.
1
分析:根据勾股定理,得AC=3;再根据直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半,得其内切圆半径是(3+4-5)÷2=1.
解答:∵∠C=90°,AB=5,BC=4,
∴AC=3,
∴内切圆半径是(3+4-5)÷2=1.
点评:掌握直角三角形的内切圆半径公式:两条直角边的和与斜边的差的一半即为直角三角形内切圆的半径.
分析:根据勾股定理,得AC=3;再根据直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半,得其内切圆半径是(3+4-5)÷2=1.
解答:∵∠C=90°,AB=5,BC=4,
∴AC=3,
∴内切圆半径是(3+4-5)÷2=1.
点评:掌握直角三角形的内切圆半径公式:两条直角边的和与斜边的差的一半即为直角三角形内切圆的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
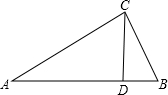 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
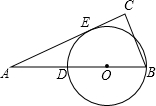 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.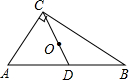 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )