题目内容
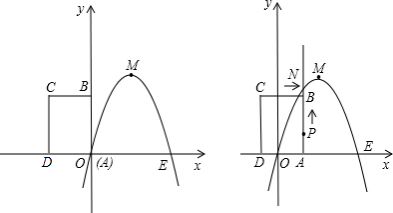
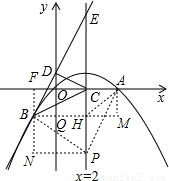
如图,已知抛物线经过原点O,与x轴交于另一点A,它的对称轴x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(m,-3),且与y轴、直线x=2分别交于点D,E.(1)求抛物线对应的函数解析式并用配方法把这个解析式化成y=a(x-h)2+k的形式;
(2)求证:CD⊥BE;
(3)在对称轴x=2上是否存在点P,使△PBE是直角三角形?如果存在,请求出点P的坐标,并求出△PAB的面积;如果不存在,请说明理由.

【答案】分析:(1)由对称轴设抛物线的解析式为y=a(x-2)2+k,由直线y=2x+1经过点B(m,-3),可以求出m的值,求出B点的坐标,从而可以求出抛物线的解析式.
(2)利用直线BE的解析式和对称轴求出E的坐标,求出CE的值,过点B作BF垂直于x轴于F,作BH垂直于直线x=2于H,交y轴于点Q,利用勾股定理可以求得△BCE是等腰三角形,且BD=DE,由等腰三角形的性质就得出结论.
(3)①当∠BPE=90°时,点P与(2)中的点H重合,可以求出P点的坐标,△PAB的面积;当∠EBP=90°时,设点P(2,y),利用△BHP∽△EHB可以求出点P的坐标,从而求出△PAB的面积.
解答:(1)解:∵已知抛物线的对称轴为x=2,
∴设抛物线的解析式为y=a(x-2)2+k,
又∵直线y=2x+1经过点B(m,-3),
∴-3=2m+1,解得,m=-2,
∴点B(-2,-3),
又∵二次函数y=a(x-2)2+k的图象经过0(0,0),B(-2,-3),
∴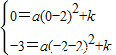 ,
,
解得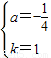 ,
,
∴抛物线的解析式为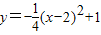 .
.
(2)证明:由题意解方程组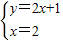 ,
,
得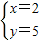
∴点E的坐标为(2,5),∴CE=5.
过点B作BF垂直于x轴于F,作BH垂直于直线x=2于H,交y轴于点Q,
∵点B(-2,-3),D(0,1),
∴BF=3,BH=4,CH=BF=3,OD=1,EH=8,DQ=4.
在Rt△BHE,Rt△BQ0,Rt△BHC中,
由勾股定理得BE=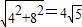 ,BD=
,BD=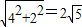 ,BC=
,BC=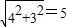
∴BD= BE,
BE,
又∵EC=5,
∴BC=CE,
∴CD⊥BE.
(3)解:结论:存在点P,使△PBE是直角三角形.
①当∠BPE=90°时,点P与(2)中的点H重合,
∴此时点P的坐标为(2,-3);
延长BH与过点A(4,0)且与x轴垂直的直线交于M,
则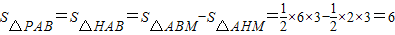 ;
;
②当∠EBP=90°时,设点P(2,y),
∵E(2,5),H(2,-3),B(-2,-3)),
∴BH=4,EH=8,PH=-3-y.
在Rt△PBE中,BH⊥PE,
可证得△BHP∽△EHB,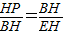 ,即
,即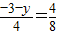 ,
,
解得y=-5,
此时点P的坐标为(2,-5).
过点P与x轴平行的直线与FB的延长线交于点N,
则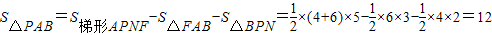 .
.
综合①,②知点P的坐标为(2,-3),△PAB的面积为6;或点P的坐标为(2,-5),△PAB的面积为12.
点评:本题是一道二次函数的综合试题,考查了待定系数法求二次函数的解析式,三角形的面积,勾股定理的运用,相似三角形的判定与性质.
(2)利用直线BE的解析式和对称轴求出E的坐标,求出CE的值,过点B作BF垂直于x轴于F,作BH垂直于直线x=2于H,交y轴于点Q,利用勾股定理可以求得△BCE是等腰三角形,且BD=DE,由等腰三角形的性质就得出结论.
(3)①当∠BPE=90°时,点P与(2)中的点H重合,可以求出P点的坐标,△PAB的面积;当∠EBP=90°时,设点P(2,y),利用△BHP∽△EHB可以求出点P的坐标,从而求出△PAB的面积.
解答:(1)解:∵已知抛物线的对称轴为x=2,
∴设抛物线的解析式为y=a(x-2)2+k,
又∵直线y=2x+1经过点B(m,-3),
∴-3=2m+1,解得,m=-2,
∴点B(-2,-3),
又∵二次函数y=a(x-2)2+k的图象经过0(0,0),B(-2,-3),
∴
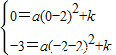 ,
,解得
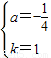 ,
,∴抛物线的解析式为
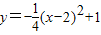 .
.(2)证明:由题意解方程组
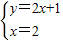 ,
,得
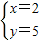
∴点E的坐标为(2,5),∴CE=5.
过点B作BF垂直于x轴于F,作BH垂直于直线x=2于H,交y轴于点Q,
∵点B(-2,-3),D(0,1),
∴BF=3,BH=4,CH=BF=3,OD=1,EH=8,DQ=4.
在Rt△BHE,Rt△BQ0,Rt△BHC中,
由勾股定理得BE=
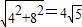 ,BD=
,BD=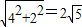 ,BC=
,BC=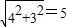
∴BD=
 BE,
BE,又∵EC=5,
∴BC=CE,
∴CD⊥BE.

(3)解:结论:存在点P,使△PBE是直角三角形.
①当∠BPE=90°时,点P与(2)中的点H重合,
∴此时点P的坐标为(2,-3);
延长BH与过点A(4,0)且与x轴垂直的直线交于M,
则
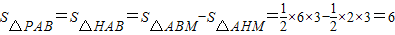 ;
;②当∠EBP=90°时,设点P(2,y),
∵E(2,5),H(2,-3),B(-2,-3)),
∴BH=4,EH=8,PH=-3-y.
在Rt△PBE中,BH⊥PE,
可证得△BHP∽△EHB,
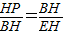 ,即
,即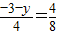 ,
,解得y=-5,
此时点P的坐标为(2,-5).
过点P与x轴平行的直线与FB的延长线交于点N,
则
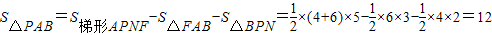 .
.综合①,②知点P的坐标为(2,-3),△PAB的面积为6;或点P的坐标为(2,-5),△PAB的面积为12.
点评:本题是一道二次函数的综合试题,考查了待定系数法求二次函数的解析式,三角形的面积,勾股定理的运用,相似三角形的判定与性质.

练习册系列答案
相关题目

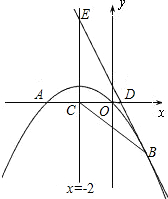 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),