题目内容
【题目】在等边![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的周长为_______.
的周长为_______.

【答案】![]()
【解析】
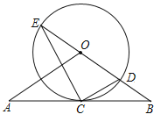
如下图,在Rt△DCF中,先求得FC,DF的值,然后在Rt△BDF中利用勾股定理可求得BD的值,接着利用旋转的性质可证△BED是正三角形,从而得出ED的长,进而得出△ADE的周长
如下图,过点D作BC的垂线,交BC于点F.
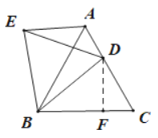
∵△ABE是△BCD绕点B逆时针旋转60°得到,AE=5
∴EB=BD,∠EBD=60°,AE=CD
∴△EBD是等边三角形,CD=AE=5,ED=BD
∵△ABC是等边三角形,BC=8,∴AC=8,∠C=60°
∴AD=AC-DC=3,在Rt△DCF中,CF=![]() ,FD=
,FD=![]()
∴BF=![]()
∴在Rt△BDF中,BD=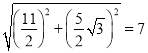
∴ED=DB=7
∴△AED的周长为:5+3+7=15
故答案为:15

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目