Question

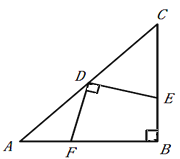
【题目】如图，在平面直角坐标系中，点B坐标为(-3，0)，点A是y轴正半轴上一点，且AB=5，点P是x轴上位于点B右侧的一个动点，设点P的坐标为（m，0）

（1）点A的坐标为( )

（2）当△ABP是等腰三角形时，求P点的坐标；

（3）如图2，过点P作PE⊥AB交线段AB于点E，连接OE．若点A关于直线OE的对称点为A'，当点A'恰好落在直线PE上时，BE=________(直接写出答案)

Answer 1

【答案】（1）0，4；（2）P点的坐标为(3，0)、 (2，0)或；（3）

【解析】

（1）在直角△AOB中，利用勾股定理求出OA，则A点坐标可知；

（2） 当△ABP为等腰三角形时，可分三种情况讨论，①若AB=AP时，利用勾股定理求出OP，则P点坐标可知；②若BA=BP，P点坐标易求；③若PA=PB时，设P（x,0）,运用两点间距离公式列式可求P点坐标.

（3）过O点作OG⊥AB，由角平分线性质定理，结合PE⊥AB，求得∠GEO=45°，再利用直角三角形的面积公式求得OG的长，则GE的长可知，利用勾股定理又可求出BG，于是BE的长可知.

（1）根据题意得：

在直角△AOB中，OA=

∴A点的坐标为（0,4）

故答案为：0，4

（2）当△ABP为等腰三角形时，分三种情况讨论

①若AB=AP=5，OP= ， ∴P(3，0)；

②若BA=BP=5，OP=BP-OB=5-3=2，∴P(2，0)；

③若PA=PB时，设P（x,0）, 则,

∴6x=7,

解得x= ，

∴P(，0)

故P点的坐标为：(3，0)、 (2，0)或(，0)

（3）如图，过O点作OG⊥AB，

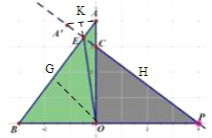
∵E在AA'的垂直平分线上，

∴∠AEK=∠A'EK，

∴∠GEO=∠OEH，

∵∠AEA'=∠BEP=90°，

∴∠GEO=45°，

∴OG=GE，

∵S△AOB=OG×AB=OA×OB，

∴OG= ，

∴GE=OG= ，

∵BG=,

∴BE=BG+GE=+=.

故答案为：.