��Ŀ����
����Ŀ����֪����x��һԪ���η���mx2+��3m+1��x+3=0�� 
��1����֤���÷���������ʵ������
��2�����������y=mx2+��3m+1��x+3��x�ύ��A��B���������㣨��A�ڵ�B��ࣩ����mΪ����������������ߵı���ʽ��
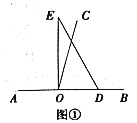
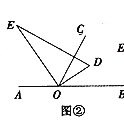
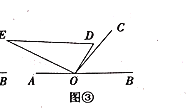
��3���ڣ�2���������£�������y=mx2+��3m+1��x+3��y�ύ�ڵ�C����B����y��ĶԳƵ�ΪD������������ک�3��x�ܩ� ![]() ֮��IJ���Ϊͼ��G�����ͼ��G����ƽ��n��n��0������λ���Ⱥ���ֱ��CD�й����㣬��n��ȡֵ��Χ��
֮��IJ���Ϊͼ��G�����ͼ��G����ƽ��n��n��0������λ���Ⱥ���ֱ��CD�й����㣬��n��ȡֵ��Χ��
���𰸡�
��1��֤�����ɸ����б�ʽ���ɵã���=��3m+1��2��4��m��3=��3m��1��2��
�ߣ�3m��1��2��0��
�����0��
��ԭ����������ʵ����
��2���⣺��y=0����ômx2+��3m+1��x+3=0��
��ã�x1=��3��x2=�� ![]() ��
��
����������x����������ĺ������Ϊ��������mΪ��������
��m=1��
�������ߵĽ���ʽΪ��y=x2+4x+3
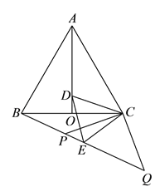
��3���⣺��ͼ��
�ߵ�x=0ʱ��y=3��
��C��0��3����
�ߵ�y=0ʱ��x1=��3��x2=��1��
�֡ߵ�A�ڵ�B����࣬
��A����3��0����B����1��0����
�ߵ�D���B����y��Գƣ�
��D��1��0����
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
�� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��CD�ı���ʽΪ��y=��3x+3��
�֡ߵ�x=�� ![]() ʱ��y=
ʱ��y= ![]() ��
��
���E���� ![]() ��
�� ![]() ����
����
��ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨��3+n��0����E�䣨�� ![]() +n��
+n�� ![]() ����
����
��ֱ��y=��3x+3������A�䣨��3+n��0��ʱ���ã���3����3+n��+3=0����ã�n=4��
��ֱ��y=��3x+3������E�䣨�� ![]() +n��
+n�� ![]() ����ʱ���ã���3����
����ʱ���ã���3���� ![]() +n��+3=
+n��+3= ![]() ����ã�n=
����ã�n= ![]() ��
��
��n��ȡֵ��Χ�� ![]() ��n��4��
��n��4��
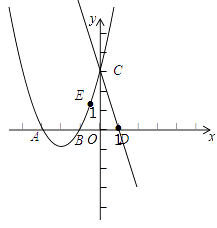
����������1������������б�ʽ�����жϡ���ȡֵ��Χ�����ɵ�֤����2�����������ʽ��ʾ�������������⣬���m��ֵ���ɵ������ߵĽ���ʽ����3���������A��B��C��D�����꣬���ݴ���ϵ�������ֱ��CD�Ľ���ʽ����ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨��3+n��0����E�䣨�� ![]() +n��
+n�� ![]() �������ݵ���ֱ���ϣ����ȡֵ��Χ���ɣ�
�������ݵ���ֱ���ϣ����ȡֵ��Χ���ɣ�

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�