��Ŀ����
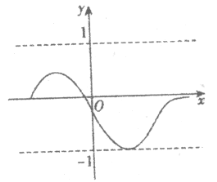
����Ŀ����ͼ1���ı���ABCD�����Σ��Խ���AC��BD�ཻ�ڵ�O��AB=2���ף���BAD=60����P��Q����ͬʱ�ӵ�O��������1����/����ٶ������εĶԽ��������˶������˶���ʱ��Ϊx�룬P��Q��ľ���Ϊy���ף�y��x�ĺ�����ϵ��ͼ�������ͼ2��ʾ����P��Q���˶�·�߿���Ϊ�� ��
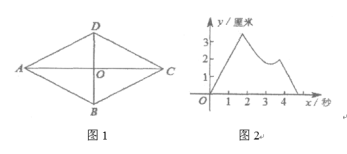
A. ��P��O��A��D��C����Q��O��C��D��O
B. ��P��O��A��B��C����Q��O��C��D��O
C. ��P��O��A��D��O����Q��O��C��D��O
D. ��P��O��A��D��O����Q��O��C��B��O
���𰸡�D
��������
�ȸ���ͼ1�в�ͬ·�ߵ�λ�ã��ж�P��Q��ľ���ı任������ٽ��ͼ2�к���ͼ��ı任���ƽ����жϷ�����
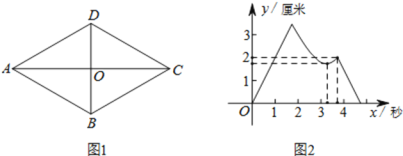
�⣺������ABCD�У�AB=2����BAD=60��
��AO=CO=![]() ��DO=BO=1
��DO=BO=1
A������P��O-A-D-C����Q��O-C-D-O����x=2+![]() ʱ��y=0����ͼ2��������A����
ʱ��y=0����ͼ2��������A����
B������P���Q�˶���ʱ����P�ڵ�C�ϣ���Q�ڵ�O�ϣ�����y=![]() ����ͼ2��������B����
����ͼ2��������B����
C������P��O-A-D-O����Q��O-C-D-O����x=2+![]() ʱ��y=0����ͼ2��������C����
ʱ��y=0����ͼ2��������C����
D������P��O-A-D-O����Q��O-C-B-O����x=![]() ʱ��y�����ֵ����x=
ʱ��y�����ֵ����x=![]() +
+![]() ʱ��y=
ʱ��y=![]() ����x=3+
����x=3+![]() ʱ��y=0����ͼ2�������D��ȷ��
ʱ��y=0����ͼ2�������D��ȷ��
��ѡ��D��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ����ijһ�������������Ŀ��СӢ��100β���˱�ǵ���Ͷ������У������������̣�ÿ�β��̺����ü�¼��Ȼ����Żأ���˽���20�Σ���¼�������£�
������ | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
����� | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
������ | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
����� | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
(1)���Ƴ���������������������ַ��������Ƿ�ȷ?
(2)�������һ�ֱ�ǵķ�����ʹ�ù��Ƹ��Ӿ���