Question

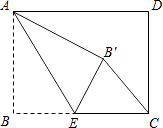
【题目】如图，平行四边形ABCD中，点E、F分别在AD、AB上，依次连接EB、EC、FC、FD，图中阴影部分的面积分别为S1、S2、S3、S4 ， 已知S1=2、S2=12、S3=3，则S4的值是 ．

Answer 1

【答案】7
【解析】解：设平行四边形的面积为S，则S△CBE=S△CDF= S， 由图形可知，△CDF面积+△CBE面积+（S1+S4+S3）﹣S2=平行四边形ABCD的面积
∴S=S△CBE+S△CDF+2+S4+3﹣12，
即S= S+ S+2+S4+3﹣12，
解得S4=7，
所以答案是：7．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)．