题目内容
【题目】E折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 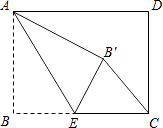
【答案】![]() 或3
或3
【解析】解:当△CEB′为直角三角形时,有两种情况: 
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC= ![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4﹣x)2 , 解得x= ![]() ,
,
∴BE= ![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述,BE的长为 ![]() 或3.
或3.
所以答案是: ![]() 或3.
或3.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
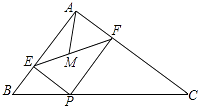
金状元绩优好卷系列答案【题目】如图,平行四边形ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4 , 已知S1=2、S2=12、S3=3,则S4的值是 . 
【题目】某公司生产某种商品每件成本为20元,这种商品在未来40天内的日销售量y(件)与时间x(天)的关系如下表:
时间x(天) | 1 | 3 | 6 | 10 | ... |
日销售量y(件) | 94 | 90 | 84 | 76 | ... |
未来40天内,前20天每天的价格m(元/件)与时间x(天)的函数关系式为![]() (1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1)分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y(件)与x(天)之间的函数关系式.
(2)当1≤x≤20时,设日销售利润为W元,求出W与x的函数关系式.
(3)在未来40天中,哪一天的日销售利润最大,最大日销售利润是多少?