题目内容
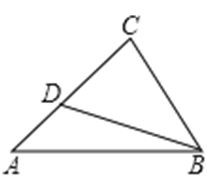
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.

(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.

(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1 S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
(1)= (2)△BCD∽△CFB∽△DEC,证明见解析
思路分析:(1)根据S1=
 S矩形BDEF,S2+S3=
S矩形BDEF,S2+S3= S矩形BDEF,即可得出答案.
S矩形BDEF,即可得出答案.(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可.
解答:(1)解:∵S1=
 BD×ED,S矩形BDEF=BD×ED,
BD×ED,S矩形BDEF=BD×ED,∴S1=
 S矩形BDEF,
S矩形BDEF,∴S2+S3=
 S矩形BDEF,
S矩形BDEF,∴S1=S2+S3.
(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.
点评:本题考查了相似三角形的判定,注意掌握相似三角形的判定定理,最经常用的就是两角法,此题难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
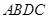 中,点
中,点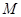 是
是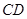 的中点,
的中点,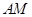 与
与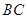 相交于点
相交于点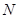 ,那么
,那么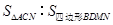 等于 .
等于 .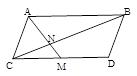
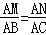 ;③△PMN为等边三角形; ④当∠ABC=45°时,BN=
;③△PMN为等边三角形; ④当∠ABC=45°时,BN=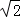 PC.其中正确的是__________.
PC.其中正确的是__________.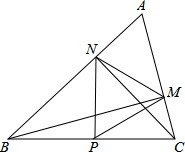
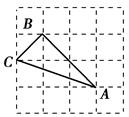
 中,
中, 为
为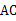 边上一点,∠
边上一点,∠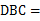 ∠
∠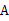 ,
,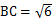 ,
,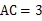 ,则
,则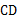 的长为( )
的长为( )