Question

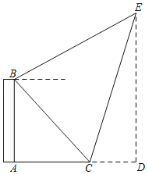
【题目】、两地相距30千米，已知甲、乙两人分别骑自行车和摩托车从地出发前往地，途中乙因修车耽误了些时间，然后又继续赶路.图5中的线段和折线分别反映了甲、乙两人所行的路程（千米）与时间（分）的函数关系，根据图像提供的信息回答下列问题：

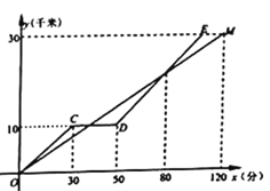
（1）甲骑自行车的速度是_________千米/分钟；

（2）两人第二次相遇时距离地________千米；

（3）线段反映了乙修好车后所行的路程（千米）与时间（分）的函数关系.请求出线段的表达式及其定义域.

Answer 1

【答案】（1）0.25；（2）20；（3）.

【解析】

（1）根据图象可以得到甲120分走的路程是30千米，由此可以求出甲骑自行车的速度；
（2）根据图象两人第二次相遇的时间是第80分钟，根据甲的速度，即可求出两人第二次相遇时距离地的距离；
（3）根据图象知道乙所行驶的路程y（千米）与行驶时间x（分钟）的函数关系式为一次函数关系，利用待定系数法即可确定，然后根据实际情况即可确定函数的定义域．

（1）根据图象可以得到甲120分走的路程是30千米，

由此甲骑自行车的速度为：千米/分钟；
故答案为0.25.

（2）根据图象两人第二次相遇的时间是第80分钟，

此时两人距离地的距离为：千米；

故答案为20.

（3）设根据图象知道乙所行驶的路程y（千米）与行驶时间x（分钟）的函数关系式为，

把(50,10)和(80,20)代入得

解得：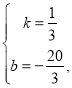

因此，乙所行驶的路程y（千米）与行驶时间x（分钟）的函数关系式为：

当时，

函数的定义域为.