Question

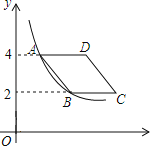
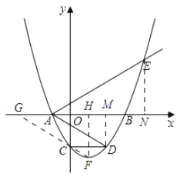
【题目】如图，二次函数（其中）的图像与轴分别交于点、（点位于的左侧），与轴交于点，过点作轴的平行线交二次函数图于点.

（1）当时，求、两点的坐标；

（2）过点作射线交二次函数的图像与点，使得，求点的坐标（用含的式子表示）

（3）在第问的条件下，二次函数的顶点为，过点、作直线与轴于点，试求出以、、的长度为三边长的三角形的面积（用含的式子表示）

Answer 1

【答案】(1)当时，，;(2)，;(3)

【解析】

(1)将代入解析式，解方程即可求得A、B两点的坐标；

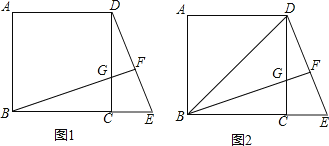
(2)过点D、E分别作x轴的垂线，首先求出A、B两点坐标，由△ADM∽△AEN，设，根据对应边成比例，即可求得答案；

(3)先求得直线FC的解析式，求得G点坐标，继而求得、、，证明它们能组成直角三角形，从而求得答案．

(1)当时，，

解方程得：

，

∴A、B两点的坐标为 ；

(2)令，则，

∴C点坐标为

令，则，

解得：，

∵点A位于B的左侧，

∴A点坐标为B点坐标为

∴抛物线的对称轴为，

∵轴，且对称轴为，

∴D点坐标为

过作轴于M，过作轴于N，

∵，

∴，

∴，

设，则，，

，，，

∴，

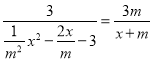解得：，

∴，

∴E点坐标为；

(3)∵对称轴为，

∴顶点F的坐标为，

设直线FC的解析式为，

则，解得：，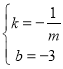

∴直线FC的解析式为：，

令，则，

∴G点坐标为

∴，

同理：，，

∵，

∴，

∴、、能构成以为斜边的直角三角形，

∵，，

∴三角形面积是．