题目内容
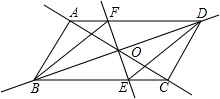
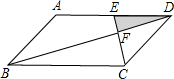 如图,平行四边形ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为________.
如图,平行四边形ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为________.
2S
分析:根据平行四边形的性质,可证△EDF∽△CBF,继而证得相似之比为EF:CF=ED:BC=1:2,所以当△DEF的面积为S时,则△DCF的面积为2S.
解答:根据平行四边形的性质知,AD=BC,AD∥BC,
∴∠EDF=∠CBF(两直线平行,内错角相等),
∠DEF=∠BCF(两直线平行,内错角相等),
∴△EDF∽△CBF(AA),
∴ED:CB=EF:CF(两三角形相似,对应边成比例);
又∵E为AD的中点,
∴ED= AD=
AD= BC,
BC,
∴EF:CF=1:2,
从图中可以看出△EDF与△DCF共一顶点D,
∴△EDF与△DCF高相等,
∴△EDF与△DCF的面积比是:EF:CF=1:2,
当△DEF的面积为S时,则△DCF的面积为2S.
故答案是:2S.
点评:本题主要考查了平行四边形的性质,相似三角形的判定及性质,及三角形面积的求法,内容比较广.
分析:根据平行四边形的性质,可证△EDF∽△CBF,继而证得相似之比为EF:CF=ED:BC=1:2,所以当△DEF的面积为S时,则△DCF的面积为2S.
解答:根据平行四边形的性质知,AD=BC,AD∥BC,
∴∠EDF=∠CBF(两直线平行,内错角相等),
∠DEF=∠BCF(两直线平行,内错角相等),
∴△EDF∽△CBF(AA),
∴ED:CB=EF:CF(两三角形相似,对应边成比例);
又∵E为AD的中点,
∴ED=
 AD=
AD= BC,
BC,∴EF:CF=1:2,
从图中可以看出△EDF与△DCF共一顶点D,
∴△EDF与△DCF高相等,
∴△EDF与△DCF的面积比是:EF:CF=1:2,
当△DEF的面积为S时,则△DCF的面积为2S.
故答案是:2S.
点评:本题主要考查了平行四边形的性质,相似三角形的判定及性质,及三角形面积的求法,内容比较广.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
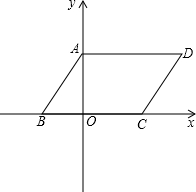 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.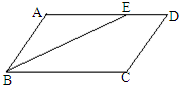 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是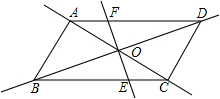
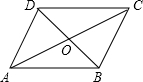 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是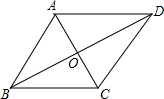 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为