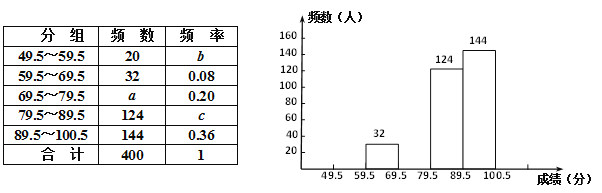
题目内容
【题目】如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,与y轴交于点C, ![]() =
= ![]() .
.
(1)求m的值;
(2)如图2,连接BC,点P为点B右侧的抛物线上一点,连接PA并延长交y轴于点D,过点P作PF⊥x轴于F,交线段CB的延长线于点E,连接DE,求证:DE∥AB;
(3)在(2)的条件下,点G在线段PE上,连接DG,若EG=2PG,∠DPE=2∠GDE时,求点P的坐标.
【答案】
(1)
解:对于抛物线y=mx2﹣6mx+5m,
令y=0,得mx2﹣6mx+5m=0,解得x=1或5,
∴A(1,0),B(5,0),
∴AB=4,
∵ ![]() =
= ![]() ,
,
∴OC=5,
∴5m=5,
∴m=1
(2)
解:如图2中,设P(t,t2﹣6t+5).
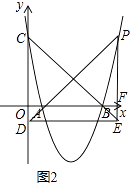
∵OC=OB=5,∠AOB=90°,
∴∠OCB=∠OBC=∠EBF=45°,
∵PE⊥AB于F,
∴△BEF是等腰直角三角形,
∴BF=EF=t﹣5,
∴点E坐标(t,5﹣t),
∵A(1,0),P(t,t2﹣6t+5),
设直线AP的解析式为y=kx+b,则有 ![]() ,
,
解得 ![]() ,
,
∴D(0,5﹣t),
∴D、E两点纵坐标相同,
∴DE∥AB
(3)
解:如图3中,在DE上截取一点M,使得DM=MG.设P(t,t2﹣6t+5).则PE=t2﹣5t.
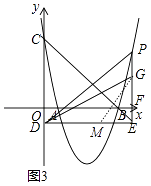
∵EG=2PG,
∴GE= ![]() (t2﹣5t),
(t2﹣5t),
∵MD=MG,设DM=MG=a,
∴∠MDG=∠MGD,
∴∠GME=2∠MDG,
∵∠DPE=2∠GDE,
∴∠DPE=∠GME,
∴tan∠DPE=tan∠GME,
∴ ![]() =
= ![]() ,
,
在Rt△MGE中,a2=(t﹣a)2+[ ![]() (t2﹣5t)]2,
(t2﹣5t)]2,
∴a= ![]() t3﹣
t3﹣ ![]() t2+
t2+ ![]() t,
t,
∴EM=t﹣a=﹣ ![]() t3+
t3+ ![]() t2﹣
t2﹣ ![]() t,
t,
∴ ![]() =
= 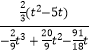 ,
,
整理得到16t2﹣160t+391=0,
解得t= ![]() 或
或 ![]() (舍弃),
(舍弃),
∴点P坐标( ![]() ,
, ![]() )
)
【解析】(1)先求出A、B两点坐标,再根据条件求出点C坐标,即可解决问题.(2)如图1中,设P(t,t2﹣6t+5),想办法求出D、E两点坐标(用t表示),只要纵坐标相同即可证明.(3)如图3中,在DE上截取一点M,使得DM=MG.设P(t,t2﹣6t+5).则PE=t2﹣5t,设DM=MG=a,在Rt△MGE中,a2=(t﹣a)2+[ ![]() (t2﹣5t)]2 , 求出a,再根据tan∠DPE=tan∠GME,得
(t2﹣5t)]2 , 求出a,再根据tan∠DPE=tan∠GME,得 ![]() =
= ![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案