题目内容
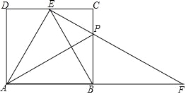
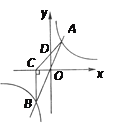
【题目】如图,直线y=kx(k>0)与双曲线y=![]() 交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=
交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据反比例函数的对称性、函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=![]() |k|及三角形中位线的判定依次分析即可.
|k|及三角形中位线的判定依次分析即可.
解:①反比例函数与正比例函数若有交点,一定是两个,且关于原点对称,②根据A、B关于原点对称,S△ABC为即A点横纵坐标的乘积,为定值1,③因为AO=BO,OD∥BC,所以OD为△ABC的中位线,即D是AC中点,所以正确;
④在△ADO中,因为AD和y轴并不垂直,所以面积不等于k的一半,即不会等于![]() ,所以错误.
,所以错误.
故选C.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目