题目内容
已知关于x的方程2x2+kx-2k+1=0的实根的平方和为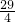 ,则k的值为
,则k的值为
- A.3
- B.11
- C.3或-11
- D.-3或11
A
分析:先设关于x的方程2x2+kx-2k+1=0的两实数根分别为x1、x2,再根据根与系数的关系得出x1+x2,x1•x2的表达式,根据方程实根的平方和为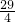 即可得出关于k的一元二次方程,求出k的值即可.
即可得出关于k的一元二次方程,求出k的值即可.
解答:设关于x的方程2x2+kx-2k+1=0的两实数根分别为x1、x2,
则x1+x2=-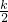 ,x1•x2=
,x1•x2=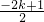 ①
①
∵原方程两实根的平方和为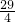 ,
,
∴x12+x22=(x1+x2)2-2x1x2=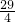 ②
②
∵方程有两实数根,
∴△=k2-4×2×(-2k+1)≥0,
∴k≥6 -8或k≤-6
-8或k≤-6 -8,
-8,
把①代入②得,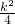 -2×
-2×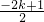 =
=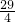 ,解得k1=3,k2=-11(舍去).
,解得k1=3,k2=-11(舍去).
∴k=3.
故选A.
点评:本题考查的是一元二次方程根与系数的关系,即若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=- ,x1x2=
,x1x2= .
.
分析:先设关于x的方程2x2+kx-2k+1=0的两实数根分别为x1、x2,再根据根与系数的关系得出x1+x2,x1•x2的表达式,根据方程实根的平方和为
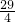 即可得出关于k的一元二次方程,求出k的值即可.
即可得出关于k的一元二次方程,求出k的值即可.解答:设关于x的方程2x2+kx-2k+1=0的两实数根分别为x1、x2,
则x1+x2=-
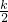 ,x1•x2=
,x1•x2=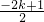 ①
①∵原方程两实根的平方和为
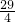 ,
,∴x12+x22=(x1+x2)2-2x1x2=
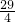 ②
②∵方程有两实数根,
∴△=k2-4×2×(-2k+1)≥0,
∴k≥6
 -8或k≤-6
-8或k≤-6 -8,
-8,把①代入②得,
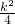 -2×
-2×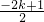 =
=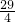 ,解得k1=3,k2=-11(舍去).
,解得k1=3,k2=-11(舍去).∴k=3.
故选A.
点评:本题考查的是一元二次方程根与系数的关系,即若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
已知关于x的方程2x-3=
+x的解满足|x|=1,则m的值是( )
| m |
| 3 |
| A、-6 | B、-12 |
| C、-6或-12 | D、6或12 |