题目内容
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知Rt△ABC中,∠B=90°,较短的一条直角边边长为1,如果Rt△ABC是“有趣三角形”,那么这个三角形“有趣中线”长等于
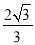 .
.
【解析】
试题分析:“有趣中线”分别三种情况,两个直角边跟斜边,而直角三角形的斜边的中点到三顶点距离相等,不符合;两个直角边,有一种情况有趣中线为1.但是不符合较短的一条直角边边长为1,只能为另一条直角边上的中线,利用勾股定理求出即可.
试题解析:“有趣中线”有三种情况:
若“有趣中线”为斜边AC上的中线,直角三角形的斜边的中点到三顶点距离相等,不合题意;
若“有趣中线”为AB边上的中线,根据斜边大于直角边,矛盾,不成立;
若“有趣中线”为另一直角边BC上的中线,如图所示,AB=1,
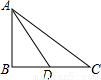
设AD=2x,则BD=x,
在Rt△ABD中,根据勾股定理得:AD2=AB2+BD2,即(2x)2=12+x2,
解得:x=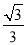 ,
,
则这个三角形“有趣中线”长等于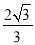 .
.
考点:勾股定理.

练习册系列答案
相关题目