题目内容
 已知:如图,割线ABC与⊙O相交于B,C两点,E是
已知:如图,割线ABC与⊙O相交于B,C两点,E是 | BC |
求证:AD是⊙O的切线.
分析:连接OE交BC于点F,连接OD,利用垂径定理,以及等边对等角,即可证得:∠ODA=90°,从而证得AC是圆的切线.
解答: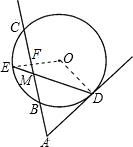 证明:连接OE交BC于点F,连接OD.
证明:连接OE交BC于点F,连接OD.
∵E是
的中点,
∴OE⊥BC,
∴∠E+∠EMF=90°,
∵∠EDA=∠AMD,
又∠AMD=∠EMF,
∴∠ADM+∠E=90°,
∵OE=OD,
∴∠FEM=∠ODE,
∴∠ODE+∠ADM=90°,即∠ODA=90°,
∴OD⊥AD,
∴AD是圆的切线.
 证明:连接OE交BC于点F,连接OD.
证明:连接OE交BC于点F,连接OD.∵E是
 |
| BC |
∴OE⊥BC,
∴∠E+∠EMF=90°,
∵∠EDA=∠AMD,
又∠AMD=∠EMF,
∴∠ADM+∠E=90°,
∵OE=OD,
∴∠FEM=∠ODE,
∴∠ODE+∠ADM=90°,即∠ODA=90°,
∴OD⊥AD,
∴AD是圆的切线.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
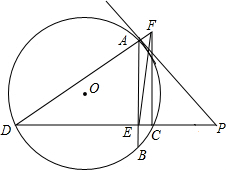 已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值.
已知,如图,PA切⊙O于点A,割线PD交⊙O于点C、D,∠P=45°,弦AB⊥PD,垂足为E,且BE=2CE,DE=6,CF⊥PC,交DA的延长线于点F.求tan∠CFE的值.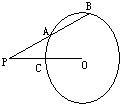 8、已知:如图⊙O的割线PAB交⊙O于点A,B,PA=7cm,AB=5cm,PO=10cm,则⊙O的半径是( )
8、已知:如图⊙O的割线PAB交⊙O于点A,B,PA=7cm,AB=5cm,PO=10cm,则⊙O的半径是( )
 22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
22、已知,如图AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.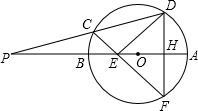 15°,⊙O的半径为2,则CF的大小为
15°,⊙O的半径为2,则CF的大小为